初三(1)班周末组织登笔架山活动.考虑到男、女同学体能的差异,分男、女两队.两队同时从山脚出发,沿同一条道路上、下山.已知男、女两队所用的时间比为2:3.
(1)直接写出男、女两队行进的速度之比;
(2)当男队到达山顶时,女队处于山腰A处,且A处离山顶尚有600米,求山脚距山顶的路程;
(3)在第(2)问所述内容(除最后的问句处)的基础上,设女队从A处继续登山,男队到达山顶后休息片刻,从原路下山,并且在山腰B处与女队相遇.请你先根据以上情景,提出一个相应的问题,再给予解答(要求:①问题的提出不能再增加其他条件;②问题的解决必须利用上述情景提供的所有已知条件).
解:(1)男、女两队行进的速度比为3:2;
(2)设山脚距山顶的路程为x米,依题意得
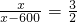
,
解得x=1800(米)
经检验,x=1800是所列方程的根.
答:山脚距山顶1800米;
(3)可提出问题“B处距山顶小于多少米?”或“男队从B处下到山脚的路程要超过多少米?”
按前面的问题,设B处与山顶路程为a米(a>0),男队速度为3k米/时,女队速度为2k米/时,依题意得
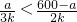
,
解得:a<360(米)
答:B处与山顶的路程小于360米.
分析:(1)所走的路程相等,那么速度之比应与所用时间之比的积应相等;
(2)根据两队所用的时间相等可得等量关系,求解即可;
(3)可从B处距离山顶的距离提问,根据男队走B处距离山顶的距离的时间小于女队走到此处的时间解答即可.
点评:综合考查了行程问题中分式方程及一元一次不等式的应用;根据时间得到的想要的关系式是解决本题的关键.

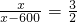 ,
,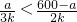 ,
,

 小学能力测试卷系列答案
小学能力测试卷系列答案