
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1.
如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4).
如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对太湖流域水质情况的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个城市每天丢弃塑料袋数量的调查 | |
| D. | 对无锡电视台某栏目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从一个不透明的袋子里面挑球,连续10次都摸出红球,那么袋子里面只有红球 | |
| B. | 天气预报“明天降水概率25%”,是指明天有25%的时间会下雨 | |
| C. | 某种福利彩票,中奖率是千分之一,买这种彩票1000张,一定会中奖 | |
| D. | 连续投一枚硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
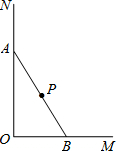 如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )
如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )| A. | 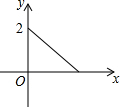 | B. | 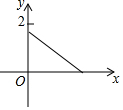 | C. | 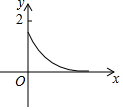 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com