
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( ) 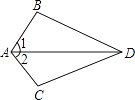
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】为了解八年级学生的课外阅读情况,我校语文组从八年级随机抽取了若干名学生,对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图,请你依据图中提供的信息,解答下列问题:(每组含最小值不含最大值)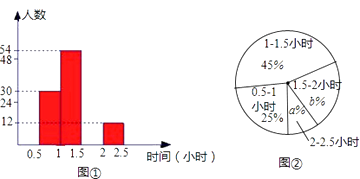
(1)从八年级抽取了多少名学生?
(2)填空(直接把答案填到横线上)
①“2-2.5小时”的部分对应的扇形圆心角为度;
②课外阅读时间的中位数落在(填时间段)内.
(3)如果八年级共有800名学生,请估算八年级学生课外阅读时间不少于1.5小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P为直线 ![]() 外一点,点A、B、C为直线
外一点,点A、B、C为直线 ![]() 上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线
上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线 ![]() 的距离为( )
的距离为( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( ). ①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB; ④点D到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离; ⑥线段AB是点B到AC的距离; ⑦AD>BD. 
A.2个
B.4个
C.7个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )

A.6 B.8 C.10 D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com