
【题目】在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.

(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
【答案】(1)四边形EGFH是平行四边形;(2)菱形;(3)菱形;(4)四边形EGFH是正方形.
【解析】
试题分析:(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
(4)当AC=BD且AC⊥BD时,四边形ABCD是正方形,则对角线相等且互相垂直平分;可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出EGFH的形状.
试题解析:(1)四边形EGFH是平行四边形;
证明:∵ABCD的对角线AC、BD交于点O
∴点O是ABCD的对称中心;
∴EO=FO,GO=HO;
∴四边形EGFH是平行四边形;
(2)∵四边形EGFH是平行四边形,EF⊥GH,
∴四边形EGFH是菱形;
(3)菱形;
由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
(4)四边形EGFH是正方形;
证明:∵AC=BD,
∴ABCD是矩形;
又∵AC⊥BD,
∴ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
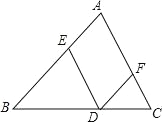
【题目】已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
(1)证明:△BDE∽△DCF;
(2)若△ABC的面积为10,点G为线段AF上的任意一点,设FC:AC=n,△DEG的面积为S,求S关于n的关系式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
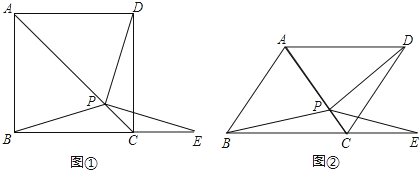
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件300元的价格卖出两件衣服,其中一件盈利25%,另一件亏损20%,那么商店卖出这两件衣服总的是( )
A. 盈利15元 B. 亏损15元 C. 盈利40元 D. 亏损40元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.(a+15%)(a-5%)万元B.(a-15%)(a+5%)万元
C.a(1+15%)(1-5%)万元D.a(1-15%)(1+5%)万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动,设两点移动的时间为t秒,回答下列问题:
(1)如图1,当t为几秒时,△PBQ的面积等于5cm2?
(2)如图2,当t=![]() 秒时,试判断△DPQ的形状,并说明理由;
秒时,试判断△DPQ的形状,并说明理由;
(3)如图3,以Q为圆心,PQ为半径作⊙Q.
①在运动过程中,是否存在这样的t值,使⊙Q正好与四边形DPQC的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若⊙Q与四边形DPQC有三个公共点,请直接写出t的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
我市交通有关部门规定:出租车起步价允许行驶的最远路程为2千米,超过2千米的部分按每千米另收费.甲说:“我乘这种出租车走了11千米,表上显示要付费19.2元”;乙说:“我乘这种出租车走了20千米,表上显示要付费35.4元”.请你算一算这种出租车的起步价是多少元?以及超过2千米后每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民用水情况,小明在某小区随机抽查了30户家庭的月用水量,结果如下表:
月用水量/m3 | 4 | 5 | 6 | 8 | 9 | 10 |
户数 | 6 | 7 | 9 | 5 | 2 | 1 |
则这30户家庭的月用水量的众数和中位数分别是( )
A.6,6
B.9,6
C.6,9
D.6,7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com