
【题目】已知,直线l1:y=﹣x+n过点A(﹣1,3),双曲线C:y= ![]() (x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.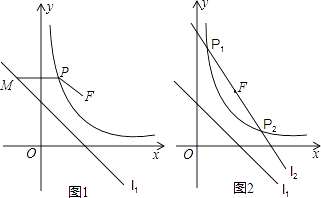
(1)求直线l1 , 双曲线C的解析式,定点F的坐标;
(2)在双曲线C上取一点P(x,y),过P作x轴的平行线交直线l1于M,连接PF.求证:PF=PM.
(3)若动直线l2与双曲线C交于P1 , P2两点,连接OF交直线l1于点E,连接P1E,P2E,求证:EF平分∠P1EP2 .
【答案】
(1)解:∵直线l1:y=﹣x+n过点A(﹣1,3),
∴﹣(﹣1)+n=3,
解得:n=2,
∴直线l1的解析式为:y=﹣x+2,
∵双曲线C:y= ![]() (x>0)过点B(1,2),
(x>0)过点B(1,2),
∴m=xy=1×2=2,
即双曲线C的解析式为:y= ![]() ,
,
∵动直线l2:y=kx﹣2k+2=k(x﹣2)+2,
∴不论k为任何负数时,当x=2时,则y=2,
即动直线l2:y=kx﹣2k+2恒过定点F(2,2)
(2)证明:如图1,在双曲线C上任取一点P(x,y),过P作x轴的平行线交直线l1于M(x0,y),连接PF.
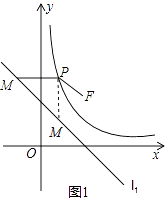
则PF=x﹣x0,
又∵M(x0,y)在直线l1上,
∴﹣x0+2=y,
∴x0=2﹣y=2﹣ ![]() ,
,
∴PM=x+ ![]() ﹣2,
﹣2,
又∵PF= ![]() =
= ![]() =
= ![]() =
= ![]() =x+
=x+ ![]() ﹣2;
﹣2;
(注:x+ ![]() ﹣2=(
﹣2=( ![]() )2+(
)2+( ![]() )2﹣2
)2﹣2 ![]()
![]() +2
+2 ![]() ﹣2=(
﹣2=( ![]() ﹣
﹣ ![]() )2+2
)2+2 ![]() ﹣2=(
﹣2=( ![]() ﹣
﹣ ![]() )2+2(
)2+2( ![]() ﹣1)≥2(
﹣1)≥2( ![]() ﹣1)>0)
﹣1)>0)
∴PM=PF;
(3)证明:证明:如图2,过P1分别作P1M1∥x轴交l1于M1,作P1N1⊥l1,垂足为N1,过P2分别作P2M2∥x轴交l1于M2,作P2N2⊥l1,垂足为N2,
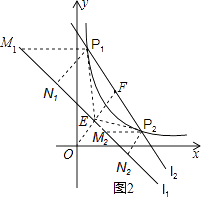
∵直线l1的解析式为y=﹣x+2,
∴△P1M1N1和△P2M2N2都是等腰直角三角形.
∴P1N1= ![]() P1M1=
P1M1= ![]() P1F,P2N2=
P1F,P2N2= ![]() P2M2=
P2M2= ![]() P2F,
P2F,
∵直线EF的解析为:y=x,
∴EF⊥l1,
∴P1N1∥EF∥P2N2,
∴ ![]() =
= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴△P1N1E∽△P2N2E,
∴∠P1EN1=∠P2EN2,
∵∠P1EF=90°﹣∠P1EN1,∠P2EF=90°﹣∠P2EN2,
∴∠P1EF=∠P2EF,
∴EF平分∠P1EP2.
【解析】(1)由直线l1:y=﹣x+n过点A(﹣1,3),双曲线C:y= ![]() (x>0),过点B(1,2),利用待定系数法即可求得直线l1,双曲线C的解析式;由动直线l2:y=kx﹣2k+2,配方法可求得定点F的坐标;(2)首先在双曲线C上任取一点P(x,y),过P作x轴的平行线交直线l1于M(x0,y),连接PF.然后分别求得PM与PF的长,继而证得结论;(3)首先过P1分别作P1M1∥x轴交l1于M1,作P1N1⊥l1,垂足为N1,过P2分别作P2M2∥x轴交l1于M2,作P2N2⊥l1,垂足为N2,易证得EF⊥l1,可得P1N1∥EF∥P2N2,继而证得△P1N1E∽△P2N2E,然后由相似三角形的对应角相等,证得结论.
(x>0),过点B(1,2),利用待定系数法即可求得直线l1,双曲线C的解析式;由动直线l2:y=kx﹣2k+2,配方法可求得定点F的坐标;(2)首先在双曲线C上任取一点P(x,y),过P作x轴的平行线交直线l1于M(x0,y),连接PF.然后分别求得PM与PF的长,继而证得结论;(3)首先过P1分别作P1M1∥x轴交l1于M1,作P1N1⊥l1,垂足为N1,过P2分别作P2M2∥x轴交l1于M2,作P2N2⊥l1,垂足为N2,易证得EF⊥l1,可得P1N1∥EF∥P2N2,继而证得△P1N1E∽△P2N2E,然后由相似三角形的对应角相等,证得结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
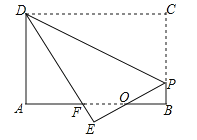
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则![]() 的值为( ).
的值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.

(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知直线![]() ,在直线
,在直线![]() 上取
上取![]() 两点,
两点,![]() 为直线
为直线![]() 上的两点,无论点
上的两点,无论点![]() 移动到任何位置都有:
移动到任何位置都有:![]() ____________
____________![]() (填“>”、“<”或“=”)
(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形![]() ,中间有条分界小路(图中折线
,中间有条分界小路(图中折线![]() ),左边区域为王爷爷的,右边区域为李爷爷的。现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由。(不计分界小路与直路的占地面积).
),左边区域为王爷爷的,右边区域为李爷爷的。现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由。(不计分界小路与直路的占地面积).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生对以下四个电视节目:![]() 最强大脑
最强大脑![]() 、
、![]() 中国诗词大会
中国诗词大会![]() 、
、![]() 朗读者
朗读者![]() 、
、![]() 出彩中国人
出彩中国人![]() 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
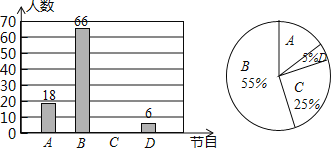
请你根据图中所提供的信息,完成下列问题:
![]() 本次调查的学生人数为______;
本次调查的学生人数为______;
![]() 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱![]() 中国诗词大会
中国诗词大会![]() 的学生有多少名.
的学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com