
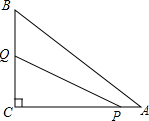
 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).分析 (1)在△ABC中,由勾股定理,求出AB的长是多少即可.
(2)首先求出AP的长度,然后用AC的长度减去AP的长度,求出CP的长度是多少即可.
(3)根据题意,分两种情况:①当0≤t≤3时;②当3<t≤8时;求出y与t之间的函数关系式即可.
(4)根据题意,分三种情况:①PC′∥BC,且点C′在AC所在的直线的上方;②PC′⊥BC;③PC′∥BC,且点C′在AC所在的直线的下方;求出直线PC′与△ABC的直角边平行或垂直时t的值各是多少即可.
解答 解:(1)如图1,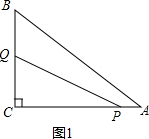
∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=$\sqrt{{8}^{2}{+6}^{2}}$=10.
(2)∵点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,
∴AP=t,
又∵AC=8,
∴CP=8-t.
(3)①如图2,当0≤t≤3时, ,
,
∵点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,
∴y=QC=2t.
②如图3,当3<t≤8时,如图,作QD⊥AC于点D,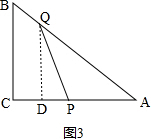 ,
,
∵sinA=$\frac{DQ}{QA}$=$\frac{BC}{AB}$=$\frac{6}{10}=\frac{3}{5}$,
∴$\frac{y}{6+10-2t}$=$\frac{3}{5}$,
∴y=-$\frac{6}{5}$t$+\frac{48}{5}$.
(4)①如图4,CC′与PQ交于点O,PC′∥BC,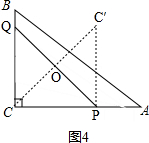 ,
,
∵点C关于直线PQ的对称点为C′,
∴CO=OC′,PC′=PC=8-t,
∵PC′∥BC,
∴$\frac{PC′}{CQ}=\frac{OC′}{CO}=1$,
∴PC′=CQ,
∴8-t=2t,
解得t=$\frac{8}{3}$.
②如图5,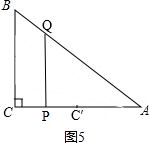 ,
,
当PQ∥BC时,点C关于直线PQ的对称点C′在线段AP上,
∴PC′⊥BC,
∵PQ∥BC,
∴$\frac{AP}{CP}=\frac{AQ}{BQ}$,
∴$\frac{t}{8-t}=\frac{6+10-2t}{2t-6}$,
解得t=$\frac{64}{13}$.
③如图6,CC′与QP的延长线交于点D,PC′∥BC,
∵点C关于直线PQ的对称点为C′,
∴CD=DC′,PC′=PC,
∵PC′∥BC,BC⊥AC,
∴PC′⊥AC,∠CPC′=90°,
∴∠CPD=45°,
又∵∠APQ=∠CPD,
∴∠APQ=45°,
∴sin∠AQP=sin(45°+∠PAQ)=$\frac{\sqrt{2}}{2}$×($\frac{6}{10}+\frac{8}{10}$)=$\frac{7\sqrt{2}}{10}$,
在△APQ中,由正弦定理,可得
$\frac{AQ}{sin45°}=\frac{AP}{sin∠AQP}$,
∴$\frac{6+10-2t}{\frac{\sqrt{2}}{2}}=\frac{t}{\frac{7\sqrt{2}}{10}}$,
解得t=$\frac{112}{19}$.
综上,可得直线PC′与△ABC的直角边平行或垂直时,t=$\frac{8}{3}$,$\frac{64}{13}$或$\frac{112}{19}$.
点评 (1)此题主要考查了相似形综合题,考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(2)此题还考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
| 人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com