
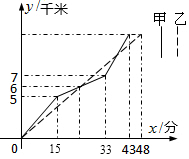
 如图表示甲、乙两名同学在”五.一环遗爱湖自行车骑行”比赛中路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题.
如图表示甲、乙两名同学在”五.一环遗爱湖自行车骑行”比赛中路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题.分析 (1)由于实线表示甲的函数图象,求得在第15到33分时甲的速度,让15分加上甲行1千米用的时间即为两人第一次相遇的时间;
(2)根据速度=路程÷时间求出乙的速度,再乘以48即为全程.
解答 解:(1)∵甲15到33分钟的速度为$\frac{7-5}{33-15}$=$\frac{1}{9}$km/min,
∴甲再行1千米用的时间为9分钟,
故当比赛开始24分时,两人第一次相遇;
(2)第一次相遇时的路程为6km,时间为24min,
所以乙的速度为6÷24=0.25km/min,
所以全长为48×0.25=12km,
故这次比赛全程是12千米.
点评 本题考查了一次函数的应用,利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决;得到甲乙两人在不同阶段内的速度是解决本题的易错点.


 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
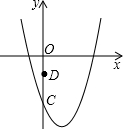 如图,抛物线y=x2-2x-3与y轴交于点C,点D的坐标为(0,-1),在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,则点P的横坐标为( )
如图,抛物线y=x2-2x-3与y轴交于点C,点D的坐标为(0,-1),在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,则点P的横坐标为( )| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1-$\sqrt{2}$或1+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 24 | C. | 30 | D. | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com