
分析 运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系:
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.
解答 解:令y=0,则-3x2-x+4=0.
∵△=(-1)2-4×(-3)×4=49>0,
∴抛物线y=-3x2-x+4与x轴的公共点有2个;
故答案为:2.
点评 此题考查了抛物线与x轴的交点.关键是掌握二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.
△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
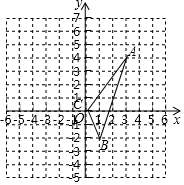 如图,已知在△ABC中任意一点P(x0,y0),经平移后对应点为P1(x0+3,y0-3),将△ABC作同样平移得到△DEF.
如图,已知在△ABC中任意一点P(x0,y0),经平移后对应点为P1(x0+3,y0-3),将△ABC作同样平移得到△DEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com