【题目】如图，一张长3x的正方形纸片，剪去两个一样的小直角三角形和一个长方形．设剪去的小长方形的长和宽分别为x，y，剪去的两个小直角三角形直角边的长也分别为x，y．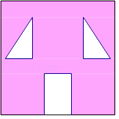 
（1）用含有x，y的式子表示图中阴影部分的面积．
（2）当x=8，y=2时，求此阴影部分的面积．
【答案】
（1）解：3x3x﹣xy﹣ 
xy×2
=9x2﹣xy﹣xy
=9x2﹣2xy
答：阴影部分的面积是9x2﹣2xy
（2）解：当x=8，y=2时，
9x2﹣2xy
=9×82﹣2×8×2
=576﹣32
=544
答：当x=8，y=2时，此阴影部分的面积是544
【解析】（1）用边长是3x的正方形的面积减去小长方形和两个小直角三角形的面积，用含有x，y的式子表示图中阴影部分的面积即可．（2）当x=8，y=2时，应用代入法，求出此阴影部分的面积是多少即可．
【考点精析】根据题目的已知条件，利用代数式求值的相关知识可以得到问题的答案，需要掌握求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入．
科目：初中数学 来源： 题型：
【题目】大双，小双的妈妈申购到一张北京奥运会的门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，各自设计一种游戏确定谁去．
大双：A袋中放着分别标有数字1，2，3的三个小球，B袋中放着分别标有数字4，5的两个小球，且都已各自搅匀，小双蒙上眼睛从两个口袋中各取出1个小球，若两个小球上的数字之积为偶数，则大双得到门票；若积为奇数，则小双得到门票．
小双：口袋中放着分别标有数字1，2，3的三个小球，且已搅匀，大双，小双各蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分；小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票．（若积分相同，则重复第二次．）
（1）大双设计的游戏方案对双方是否公平？请你运用列表或树状图说明理由；
（2）小双设计的游戏方案对双方是否公平？不必说理．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校体育课进行定点投篮比赛，10位同学参加，每人连续投5次，投中情况统计如下：
投中球数量（个） | 2 | 3 | 4 | 5 |
人数（人） | 1 | 4 | 3 | 2 |
这10位同学投中球数量的众数和中位数分别是（ ）
A. 4, 2 B. 3，4 C. 2，3.5 D. 3，3.5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若二次函数y=﹣x2+6x+c的图象过点A（﹣1，y1），B（1，y2），C（4，y3）三点，则y1 ， y2 ， y3的大小关系是（ ）
A.y1＞y2＞y3
B.y2＞y1＞y3
C.y3＞y2＞y1
D.y3＞y1＞y2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某景区在“春节”假期间，每天接待的游客人数统计如下：(单位：万人)
农历 | 十二月三十 | 正月初一 | 正月初二 | 正月初三 | 正月初四 | 正月初五 | 正月初六 |
人数 | 1.2 | 2.3 | 2 | 2.3 | 1.2 | 2.3 | 0.6 |
表中表示人数的一组数据中，众数和中位数分别是______和_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
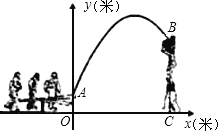
【题目】杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线y=
x2+3x+1的一部分，如图所示．
（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC=3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com