练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某校学生来自甲、乙、丙三个地区，其人数比为2∶3∶5，如图所示的扇形图表示上述分布情况．已知来自甲地区的为180人，则下列说法不正确的是 (　　)

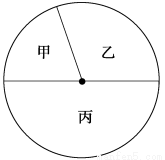
    A．扇形甲的圆心角是72°

    B．学生的总人数是900人

    C．丙地区的人数比乙地区的人数多180人

    D．甲地区的人数比丙地区的人数少180人

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙教版八年级数学上册基础训练：4.2 平面直角坐标系（二） 题型：解答题

    在平面直角坐标系中，A，B，C三点的位置如图所示，若点A，B，C的横坐标之和为a，纵坐标之和为b，求a－b的值．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上册 3.2 用频率估计概率 综合练习 题型：解答题

    (满分l2分)甲、乙两同学开展“投球进筐”比赛，双方约定：①比赛分6局进行，每局在指定区域内将球投向筐中，只要投进一次后该局便结束；②若一次未进可再投第二次，依此类推，但每局最多只能投8次，若8次投球都未进，该局也结束；③计分规则如下：a．得分为正数或0；b．若8次都未投进，该局得分为0；C．投球次数越多，得分越低；d．6局比赛的总得分高者获胜．

    (1)设某局比赛第n(n=l，2，3，4，5，6，7，8)次将球投进，请你按上述约定，用公式、表格或语言叙述等方式，为甲、乙两位同学制定一个把挖换算为得分M的计分方案；

    (2)若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数，“×”表示该局比赛8次投球都未进)：

    第一局

    第二局

    第三局

    第四局

    第五局

    第六局

    田

    5

    ×

    4

    8

    1

    3

    乙

    8

    2

    4

    2

    6

    ×

    根据上述计分规则和你制定的计分方案，确定两人谁在这次比赛中获胜．

    查看答案和解析>>

    科目：初中数学 来源：人教七年级下册数学第十章数据的收集、整理与描述单元测试卷（含答案） 题型：填空题

    在扇形统计图中，某部分占总体的百分比为25％，则该部分所对圆心角的度数为____度。

    查看答案和解析>>

    科目：初中数学 来源：人教七年级下册数学第十章数据的收集、整理与描述单元测试卷（含答案） 题型：选择题

    在-（-3），（-3）2，（-3）3，︱-3︱中，负数出现的频率为（ ）

    A. 25％ B. 50％ C. 75％ D. 100％

    查看答案和解析>>

    科目：初中数学 来源：2018届华师大版九年级数学下册：第26章检测卷 题型：解答题

    九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：

    售价（元/件）

    100

    110

    120

    130

    ……

    月销量（件）

    200

    180

    160

    140

    ……

    (1)已知该运动服的进价为每件60元，设售价为x元；

    请用含有x的式子表示：

    ①销售该运动服每件的利润是 元；

    ②月销售量是 件；（直接写结果）

    (2)设销售该运动服的月利润为y元，那么售价为多少元时，当月的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源：2018届华师大版九年级数学下册：第26章检测卷 题型：填空题

    2017年7月1日是香港回归祖国和香港特别行政区成立二十周年的大日子，特区政府为此设计了六个充满活力的时尚图像．小明挑选了他最喜欢的一个图像制作了一张如图所示的贺卡．贺卡的宽为xcm，长为40cm，左侧图片的长比宽多4cm.若14≤x≤16，则右侧留言部分的最大面积为________cm2.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学下册第17章勾股定理单元测试卷 题型：解答题

    清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日，西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”.用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，设其面积为S，则第一步： ＝m；第二步： ＝k；第三步：分别用3、4、5乘以k，得三边长”.

    （1）当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；

    （2）你能证明“积求勾股法”的正确性吗？请写出证明过程.

    查看答案和解析>>

    科目：初中数学 来源：重庆市九龙坡区七校联考2017-2018学年八年级上学期素质测查（一）数学试卷 题型：选择题

    若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角的度数为（ ）

    A． 50° B． 80° C． 65°或50° D． 50°或80°

    查看答案和解析>>

    同步练习册答案