
”¾ĢāÄæ”æĪŖÓ½Ó4ŌĀ23ČÕµÄŹĄ½ē¶ĮŹéČÕ£¬Ä³ŹéµźÖʶØĮĖ»ī¶Æ¼Ę»®£¬Čē±ķŹĒ»ī¶Æ¼Ę»®µÄ²æ·ÖŠÅĻ¢£ŗ
(1)Ńī¾Ąķ²éæ“¼Ę»®Ź±·¢ĻÖ£ŗAĄąĶ¼ŹéµÄ±ź¼ŪŹĒBĄąĶ¼Źé±ź¼ŪµÄ1.5±¶.Čō¹ĖæĶÓĆ540ŌŖ¹ŗĀņĶ¼Źé£¬Äܵ„¶Ą¹ŗĀņAĄąĶ¼ŹéµÄŹżĮæĒ”ŗƱȵ„¶Ą¹ŗĀņBĄąĶ¼ŹéµÄŹżĮæÉŁ10±¾.ĒėĒó³öA”¢BĮ½ĄąĶ¼ŹéµÄ±ź¼Ū.
(2)¾ŹŠ³”µ÷²éŗó£¬Ńī¾Ąķ·¢ĻÖĖūĆĒøß¹ĄĮĖ”°¶ĮŹéČÕ”±¶ŌĶ¼ŹéĻśŹŪµÄÓ°Ļģ£¬±ćµ÷ÕūĮĖĻśŹŪ·½°ø£ŗAĄąĶ¼ŹéĆæ±¾°“±ź¼Ū½µµĶaŌŖ(![]() )ĻśŹŪ£¬BĄąĶ¼Źé¼Ūøń²»±ä.ÄĒĆ“ŹéµźÓ¦ČēŗĪ½ų»õ²ÅÄÜ»ńµĆ×ī“óĄūČó.
)ĻśŹŪ£¬BĄąĶ¼Źé¼Ūøń²»±ä.ÄĒĆ“ŹéµźÓ¦ČēŗĪ½ų»õ²ÅÄÜ»ńµĆ×ī“óĄūČó.
”¾“š°ø”æ(1)A”¢BĮ½ĄąĶ¼ŹéµÄ±ź¼Ū·Ö±šŹĒ27ŌŖ”¢18ŌŖ£»(2)µ±Źéµź½ųAĄą600±¾£¬BĄą200±¾Ź±£¬Źéµź»ń×ī“óĄūČó.
”¾½āĪö”æ
£Ø1£©ĻČÉčBĄąĶ¼ŹéµÄ±ź¼ŪĪŖxŌŖ£¬ŌņÓÉĢāŅāæÉÖŖAĄąĶ¼ŹéµÄ±ź¼ŪĪŖ1.5xŌŖ£¬Č»ŗóøł¾ŻĢāŅāĮŠ³ö·½³Ģ£¬Ēó½ā¼“æÉ£®
£Ø2£©ĻČÉč¹ŗ½ųAĄąĶ¼Źém±¾£¬×ÜĄūČóĪŖwŌŖ£¬Ōņ¹ŗ½ųBĄąĶ¼ŹéĪŖ£Ø800-m£©±¾£¬øł¾ŻĢāÄæÖŠĖłøųµÄŠÅĻ¢ĮŠ³ö²»µČŹ½×飬Ēó³ömµÄȔֵ·¶Ī§£¬Č»ŗóøł¾Ż×ÜĄūČów=×ÜŹŪ¼Ū-×ܳɱ¾£¬Ēó³ö×ī¼ŃµÄ½ų»õ·½°ø£®
½ā£ŗ(1)ÉčBĄąĶ¼ŹéµÄ±ź¼ŪĪŖxŌŖ£¬ŌņAĄąĶ¼ŹéµÄ±ź¼ŪĪŖ1.5xŌŖ£¬ŌņæÉĮŠ·½³Ģ
![]()
½āµĆ£ŗx=18
¾¼ģŃé£ŗx=18ŹĒŌ·ÖŹ½·½³ĢµÄ½ā
ŌņA”¢BĮ½ĄąĶ¼ŹéµÄ±ź¼Ū·Ö±šŹĒ27ŌŖ”¢18ŌŖ
(2)ÉčAĄą½ų»õm±¾£¬ŌņBĄą½ų»õ(800-m)±¾£¬ĄūČóĪŖWŌŖ.
ÓÉĢāÖŖ£ŗ![]()
½āµĆ£ŗ![]() .
.
W=(27-a-18)m+(18-12)(800-m)=(3-a)m+4800
ӧ![]()
”ą![]()
”ąWĖęmµÄŌö“ó¶ųŌö“ó
”ąµ±m=600Ź±£¬WČ”×ī“óÖµ
Ōņµ±Źéµź½ųAĄą600±¾£¬BĄą200±¾Ź±£¬Źéµź»ń×ī“óĄūČó



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
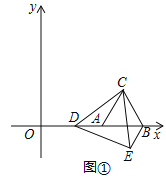
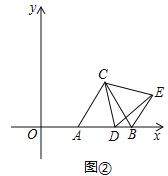
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µČ±ß”÷ABCµÄ¶„µćA£¬BµÄ×ų±ź·Ö±šĪŖ£Ø5£¬0£©£¬£Ø9£¬0£©£¬µćDŹĒxÖįÕż°ėÖįÉĻŅ»øö¶Æµć£¬Į¬½ÓCD£¬½«”÷ACDČʵćCÄꏱÕėŠż×Ŗ60”ćµĆµ½”÷BCE£¬Į¬½ÓDE£®
£Ø¢ń£©Ö±½ÓŠ“³öµćCµÄ×ų±ź£¬²¢ÅŠ¶Ļ”÷CDEµÄŠĪד£¬ĖµĆ÷ĄķÓÉ£»
£Ø¢ņ£©ČēĶ¼¢Ś£¬µ±µćDŌŚĻ߶ĪABÉĻŌĖ¶ÆŹ±£¬”÷BDEµÄÖܳ¤ŹĒ·ń“ęŌŚ×īŠ”Öµ£æČō“ęŌŚ£¬Ēó³ö”÷BDEµÄ×īŠ”Öܳ¤¼°“ĖŹ±µćDµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø¢ó£©µ±”÷BDEŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćDµÄ×ų±ź£®£ØÖ±½ÓŠ“³ö½į¹ū¼“æÉ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø12·Ö£©ČēĶ¼¢Ł£¬”ĻQPNµÄ¶„µćPŌŚÕż·½ŠĪABCDĮ½Ģõ¶Ō½ĒĻߵĽ»µć“¦£¬”ĻQPN=¦Į£¬½«”ĻQPNČʵćPŠż×Ŗ£¬Šż×Ŗ¹ż³ĢÖŠ”ĻQPNµÄĮ½±ß·Ö±šÓėÕż·½ŠĪABCDµÄ±ßADŗĶCD½»ÓŚµćEŗĶµćF£ØµćFÓėµćC£¬D²»ÖŲŗĻ£©£®
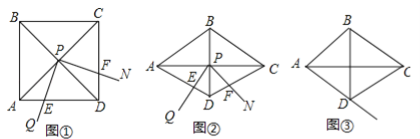
£Ø1£©ČēĶ¼¢Ł£¬µ±¦Į=90”揱£¬DE£¬DF£¬ADÖ®¼äĀś×ćµÄŹżĮæ¹ŲĻµŹĒ £»
£Ø2£©ČēĶ¼¢Ś£¬½«Ķ¼¢ŁÖŠµÄÕż·½ŠĪABCDøÄĪŖ”ĻADC=120”ćµÄĮāŠĪ£¬ĘäĖūĢõ¼ž²»±ä£¬µ±¦Į=60”揱£¬£Ø1£©ÖŠµÄ½įĀŪ±äĪŖDE+DF=![]() AD£¬Ēėøų³öÖ¤Ć÷£»
AD£¬Ēėøų³öÖ¤Ć÷£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ČōŠż×Ŗ¹ż³ĢÖŠ”ĻQPNµÄ±ßPQÓėÉäĻßAD½»ÓŚµćE£¬ĘäĖūĢõ¼ž²»±ä£¬Ģ½¾æŌŚÕūøöŌĖ¶Æ±ä»Æ¹ż³ĢÖŠ£¬DE£¬DF£¬ADÖ®¼äĀś×ćµÄŹżĮæ¹ŲĻµ£¬Ö±½ÓŠ“³ö½įĀŪ£¬²»ÓĆ¼ÓŅŌÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖŌŚŅ»Ģõ±ŹÖ±µÄµĄĀ·ÉĻĻąĻņ¶ųŠŠ£¬¼×Ęļ×ŌŠŠ³µ“ÓAµŲµ½BµŲ£¬ŅŅ¼Ż³µ“ÓBµŲµ½AµŲ£¬ĖūĆĒ·Ö±šŅŌ²»Ķ¬µÄĖŁ¶ČŌČĖŁŠŠŹ».ŅŃÖŖ¼×ĻČ³ö·¢6·ÖÖÓŗó£¬ŅŅ²Å³ö·¢£¬ŌŚÕūøö¹ż³ĢÖŠ£¬¼×”¢ŅŅĮ½ČĖµÄ¾ąĄėy(Ē§Ć×)Óė¼×³ö·¢µÄŹ±¼äx(·Ö)Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬µ±ŅŅµ½“ļÖÕµćAŹ±£¬¼×»¹Šč( )·ÖÖÓµ½“ļÖÕµćB.
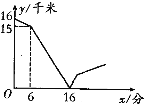
A. 78B. 76C. 16D. 12
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
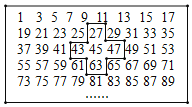
”¾ĢāÄæ”æČēĶ¼£¬½«Į¬ŠųµÄĘꏿ1£¬3£¬5£¬7””ÅųÉČēĻĀµÄŹż±ķ£¬ÓĆŹ®×ÖŠĪæņæņ³ö5øöŹż£®
Ģ½¾æ¹ęĀÉŅ»£ŗÉ菮×ÖæņÖŠ¼äµÄĘꏿĪŖx£¬ŌņæņÖŠĪåøöĘꏿµÄŗĶÓĆŗ¬xµÄÕūŹ½±ķŹ¾ĪŖ”” ””£¬ÕāĖµĆ÷±»Ź®×ÖæņæņÖŠµÄĪåøöĘꏿµÄŗĶŅ»¶ØŹĒÕżÕūŹżn£Øn£¾1£©µÄ±¶Źż£¬ÕāøöÕżÕūŹżnŹĒ”” ””£»
Ģ½¾æ¹ęĀɶž£ŗĀäŌŚŹ®×ÖæņÖŠ¼äĒŅĪ»ÓŚµŚ¶žĮŠµÄŅ»×éĘꏿŹĒ21£¬39£¬57£¬75£¬”£¬ŌņÕāŅ»×鏿æÉŅŌÓĆÕūŹ½±ķŹ¾ĪŖ18m+3£ØmĪŖŠņŹż£©£¬Ķ¬Ńł£¬ĀäŌŚŹ®×ÖæņÖŠ¼äĒŅĪ»ÓŚµŚČżĮŠµÄŅ»×éĘꏿæÉŅŌ±ķŹ¾ĪŖ”” ””£»£ØÓĆŗ¬mµÄŹ½×Ó±ķŹ¾£©
ŌĖÓĆ¹ęĀÉ£ŗ
£Ø1£©ŅŃÖŖ±»Ź®×ÖæņæņÖŠµÄĪåøöĘꏿµÄŗĶĪŖ2025£¬ŌņŹ®×ÖæņÖŠ¼äµÄĘꏿŹĒ”” ””£¬ÕāøöĘꏿĀäŌŚ“Ó×óĶłÓŅµŚ”” ””ĮŠ£»
£Ø2£©±»Ź®×ÖæņæņÖŠµÄĪåøöĘꏿµÄŗĶæÉÄÜŹĒ2020Āš£æČōÄÜ£¬ĒėĒó³öÕāĪåøöŹż£ŗČō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŅŃÖŖÖ±ĻßABµÄŗÆŹż½āĪöŹ½ĪŖy=©2x+8£¬ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£®
£Ø1£©ĒóA”¢BĮ½µćµÄ×ų±ź£»
£Ø2£©ČōµćP£Øm£¬n£©ĪŖĻ߶ĪABÉĻµÄŅ»øö¶Æµć£ØÓėA”¢B²»ÖŲŗĻ£©£¬×÷PE”ĶxÖįÓŚµćE£¬PF”ĶyÖįÓŚµćF£¬Į¬½ÓEF£¬ĪŹ£ŗ
¢ŁČō”÷PAOµÄĆ껿ĪŖS£¬ĒóS¹ŲÓŚmµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ömµÄȔֵ·¶Ī§£»
¢ŚŹĒ·ń“ęŌŚµćP£¬Ź¹EFµÄÖµ×īŠ”£æČō“ęŌŚ£¬Ēó³öEFµÄ×īŠ”Öµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
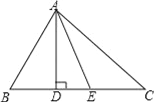
”¾ĢāÄæ”æ£Ø8·Ö£©ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AD”ĶBCÓŚD£¬AEĘ½·Ö”ĻDAC£¬”ĻBAC=80”ć£¬”ĻB=60”ć£¬Ēó”ĻAECµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
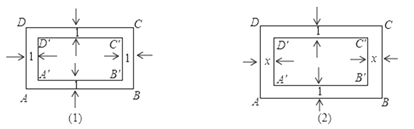
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDµÄ³¤AB=30£¬æķBC=20£®
£Ø1£©ČēĶ¼£Ø1£©ČōŃŲ¾ŲŠĪABCDĖÄÖÜÓŠæķĪŖ1µÄ»·ŠĪĒųÓņ£¬Ķ¼ÖŠĖłŠĪ³ÉµÄĮ½øö¾ŲŠĪABCDÓėA”äB”äC”äD”äĻąĖĘĀš£æĒėĖµĆ÷ĄķÓÉ£»
£Ø2£©ČēĶ¼£Ø2£©£¬xĪŖ¶ąÉŁŹ±£¬Ķ¼ÖŠµÄĮ½øö¾ŲŠĪABCDÓėA”äB”äC”äD”äĻąĖĘ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōm£¬n£¬pĀś×ćm£n£½8£¬mn£«p2£«16£½0£¬Ēóm£«n£«pµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com