
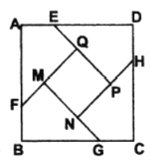
【题目】如图,在正方形![]() 各边上分别截取
各边上分别截取![]() ,且
,且![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() .四边形
.四边形![]() 面积为
面积为![]() ,当
,当![]() ,且
,且![]() 时,则
时,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如图,分别延长BA、PE交于R,QF、CB交于S,MG、DC交于T,NH、AD交于U,得到则![]() 都是全等的等腰直角三角形, 若将上述四个等腰直角三角形拼成一个新正方形,则新正方形面积与正方形ABCD面积相等,由题意得
都是全等的等腰直角三角形, 若将上述四个等腰直角三角形拼成一个新正方形,则新正方形面积与正方形ABCD面积相等,由题意得![]() 也是全等的等腰直角三角形,得到
也是全等的等腰直角三角形,得到![]() ,根据已知推出
,根据已知推出![]() ,相似比为
,相似比为![]() , 设AE=AR=x,根据相似列方程,即可求解.
, 设AE=AR=x,根据相似列方程,即可求解.
解:如图,分别延长BA、PE交于R,QF、CB交于S,MG、DC交于T,NH、AD交于U,
则![]() 都是全等的等腰直角三角形, 若将上述四个等腰直角三角形拼成一个新正方形,则新正方形面积与正方形ABCD面积相等,
都是全等的等腰直角三角形, 若将上述四个等腰直角三角形拼成一个新正方形,则新正方形面积与正方形ABCD面积相等,
由题意得![]() 也是全等的等腰直角三角形,
也是全等的等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设AE=AR=x,则![]() ,
,
![]() ,
,
解得 ![]() .
.

故选:A


科目:初中数学 来源: 题型:
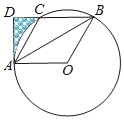
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠病毒(2019-nCoV是一种新的Sarbecovirus亚属的![]() 冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).
冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).![]() ,100nm用科学记数法可以表示为( )m.
,100nm用科学记数法可以表示为( )m.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
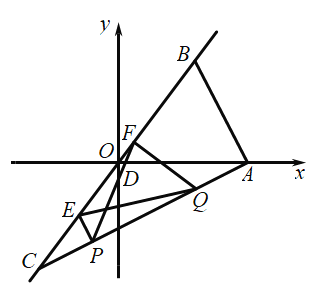
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在直线
在直线![]() 上,且
上,且![]() 是
是![]() 的中点,点
的中点,点![]() 的坐标为
的坐标为![]() .点
.点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,且
点运动,且![]() .
.
(1)求![]() 的长及点
的长及点![]() 的坐标.
的坐标.
(2)作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,设
,设![]() .
.
①在![]() ,
,![]() 相遇前,用含
相遇前,用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
②当![]() 为何值时,
为何值时,![]() 与坐标轴垂直.
与坐标轴垂直.
(3)若![]() 交
交![]() 轴于点
轴于点![]() ,除点
,除点![]() 与点
与点![]() 重合外,
重合外,![]() 的值是否为定值,若是,请直接写出
的值是否为定值,若是,请直接写出![]() 的值,若不是,请直接写出它的取值范围.
的值,若不是,请直接写出它的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() .
.
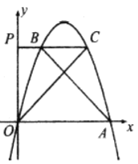
(1)求点![]() 的坐标和该抛物线的对称轴.
的坐标和该抛物线的对称轴.
(2)点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 轴交抛物线于点
轴交抛物线于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),设
的左侧),设![]() ,
,
①当![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
②连结![]() ,设
,设![]() 与
与![]() 的周长之差为
的周长之差为![]() ,求
,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
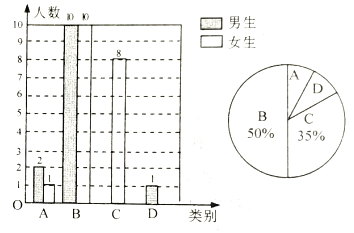
【题目】为了了解停课不停学,期间,同学们居家学习的情况,某校从全校学生中随机抽取部分学生进行网络问卷调查,并将调查结果分成(![]() :优,
:优,![]() :良,
:良,![]() :中,
:中,![]() :差)四类.依据调查结果绘制成两幅不完整的统计图
:差)四类.依据调查结果绘制成两幅不完整的统计图
(1)这次被调查的学生一共有 人,其中![]() (中)等次的男生有 人,表示
(中)等次的男生有 人,表示![]() (差)等次的扇形所对的圆心角的度数为 度;
(差)等次的扇形所对的圆心角的度数为 度;
(2)若该校约有![]() 名学生,估计全校居家学习处于优或良(
名学生,估计全校居家学习处于优或良(![]() 或
或![]() )等次的学生有多少人?
)等次的学生有多少人?
(3)为了共同进步,刘老师想从被调查的![]() 类和
类和![]() 类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
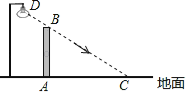
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com