
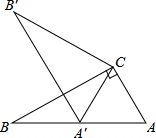
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )| A. | 150° | B. | 90° | C. | 60° | D. | 30° |
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{3x}$ | B. | $\frac{4x}{{x}^{2}+3x}$ | C. | $\frac{x+2}{{x}^{2}+4}$ | D. | $\frac{3-x}{x-3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=6}\\{x=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+y=5}\\{2x-5y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3}\\{xy=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.
如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com