
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先利用二次根式的乘法法则运算,然后化简后合并即可.
解答 解:(1)原式=5$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$
=$\frac{25\sqrt{3}}{3}$;
(2)原式=a2$\sqrt{27{a}^{3}•\frac{3}{a}}$-$\frac{a}{4}$$\sqrt{27{a}^{3}•\frac{a}{3}}$
=9a3-$\frac{3{a}^{3}}{4}$
=$\frac{33}{4}$a3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


科目:初中数学 来源: 题型:填空题
 如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.
如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
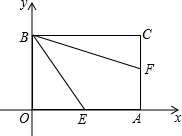 如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}-{c}^{2}}$ | C. | $\sqrt{{a}^{2}-{b}^{2}+{c}^{2}}$ | D. | $\sqrt{-{c}^{2}+{b}^{2}+{a}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com