
【题目】如果等腰三角形一腰上的高与另一腰的夹角45°,那么这个等腰三角形的底角为( )
A. 67°50′B. 22°C. 67.5°D. 22.5°或67.5°
【答案】D
【解析】
先知三角形有两种情况(1)(2),求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数.
有两种情况;
(1)如图当△ABC是锐角三角形时,BD⊥AC于D,
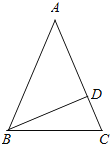
则∠ADB=90°,
已知∠ABD=45°,
∴∠A=90°-45°=45°,
∵AB=AC,
∴∠ABC=∠C=![]() ×(180°-45°)=67.5°;
×(180°-45°)=67.5°;
(2)如图,当△EFG是钝角三角形时,FH⊥EG于H,
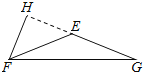
则∠FHE=90°,
已知∠HFE=45°,
∴∠HEF=90°-45°=45°,
∴∠FEG=180°-45°=135°,
∵EF=EG,
∴∠EFG=∠G=![]() ×(180°-135°)=22.5°,
×(180°-135°)=22.5°,
综合(1)(2)得:等腰三角形的底角是67.5°或22.5°,
故选D.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某校初三学生组织甲、乙两个旅行团去某景点旅游,已知甲团人数少于50人,乙团人数不超过100人.下面是小明与其他两位同学交流的情况.根据他们的对话,组织者算了一下,若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.



(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一组数据x1,x2,…,xn中,各数据与它们的平均数![]() 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T=![]() (|x1-
(|x1-![]() |+|x2-
|+|x2-![]() |+…+|xn-
|+…+|xn-![]() |)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
一水产养殖户李大爷要了解鱼塘中鱼的质量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况.为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度的几个量中某些值超标时就要捕捞,分开养殖或出售.他从甲、乙两个鱼塘各随机捕捞10条鱼称得质量(单位:千克)如下:
甲鱼塘:3、5、5、5、7、7、5、5、5、3
乙鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算从甲、乙两个鱼塘中抽取的10条鱼的质量的极差(极差:最大值与最小值的差)、方差、平均差.完成下面的表格:
极差(千克) | 方差 | 平均差(千克) | |
甲鱼塘 | |||
乙鱼塘 |
(2)如果你是技术人员,你会告诉李大爷哪个鱼塘的风险更大些?哪些量更能说明鱼质量的离散程度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据: ![]() ,
, ![]() )
)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.
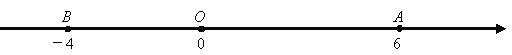
查看答案和解析>>
科目:初中数学 来源: 题型:
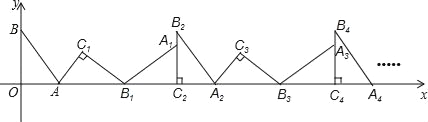
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com