
【题目】为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,做好师生返校前的卫生安全防护教育,上好开学第一课,省教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七、八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:
收集数据
八年级:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
七年级:
80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
整理数据
成绩 |
|
|
|
|
八年级 | 2 | 5 |
|
|
七年级 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
八年级 | 85.75 | 87.5 |
|
七年级 | 83.5 |
| 80 |
应用数据
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)看完统计数据,你认为对新型冠状病毒肺炎防护知识掌握更好的年级是__________;
(3)若八年级共有500人参与答卷,请估计八年级成绩大于90分的人数;
(4)在这次测试中,八年级学生甲与七年级学生乙的成绩都是85分,请判断两人在各自年级的排名谁更靠前,并说明理由.
【答案】(1)8,5,90,82.5;(2)八年级;(3)125;(4)七年级学生乙在本年级的排名更靠前,理由见解析.
【解析】
(1)由数据收集表可以得到![]() 的答案,由中位数与众数的概念得到
的答案,由中位数与众数的概念得到![]() 的答案,
的答案,
(2)由平均数,中位数,众数的数据进行分析可得到答案,
(3)利用样本估计总体即可得到答案,
(4)利用两个年级学生成绩的中位数可得到答案.
解:(1)由数据统计表得到:![]()
把八年级的成绩重新排列如下:65,70,75,75,80,80,80,85,85,85,90,90,90,90,90,95,95,95,100,100.
所以:![]() 分,
分,
把七年级的成绩重新排列如下:60,65, 70,75,75,80,80,80,80,80,85,85,90,90,90,95,95,95,100,100,
排在最中间的两个数是![]() ,所以
,所以![]() 分.
分.
故答案为:8,5,90,82.5;
(2)从平均数,中位数,众数来看,八年级都比七年级高,所以八年级对新型冠状病毒肺炎防护知识掌握更好.
故答案为:八年级.
(3)因为![]() 人中八年级成绩大于90分的人数有
人中八年级成绩大于90分的人数有![]() 人:
人:
所以估计500人中有:![]() (人).
(人).
答:估计八年级成绩大于90分的人数是125人.
(4)七年级学生乙在本年级的排名更靠前.
理由:∵八年级的中位数是87.5,七年级的中位数是![]() ,
,![]() ,
,![]() ,
,
∴在这次测试中,七年级学生乙在年级的排名更靠前.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
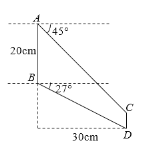
【题目】某校航模小组打算制作模型飞机,设计了如图所示的模型飞机机翼图纸.图纸中AB∥CD,均与水平方向垂直,机翼前缘AC、机翼后缘BD与水平方向形成的夹角度数分别为45°、27°,AB=20cm,点D到直线AB的距离为30cm.求机翼外缘CD的长度.(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
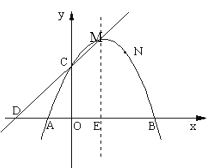
(1)求抛物线的解析式及点A、B、C的坐标;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,探索并判断四边形CDAN是怎样的四边形?并对你得到的结论予以证明;
(3)直线y=mx+2与抛物线交于T,Q两点.是否存在这样的实数m,使以线段TQ为直径的圆恰好过坐标原点,若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
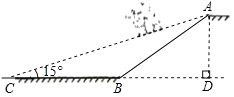
【题目】若商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,扶梯AB的坡度i为1:![]() .改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
.改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,正方形
,正方形![]() 的边长为2,将正方形
的边长为2,将正方形![]() 绕点
绕点![]() 旋转一周,连接
旋转一周,连接![]() 、
、![]() 、
、![]() .
.
(1)猜想:![]() 的值是__________,直线
的值是__________,直线![]() 与直线
与直线![]() 相交所成的锐角度数是__________;
相交所成的锐角度数是__________;
(2)探究:直线![]() 与
与![]() 垂直时,求线段
垂直时,求线段![]() 的长;
的长;
(3)拓展:取![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出线段
,直接写出线段![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,且AD=AC.

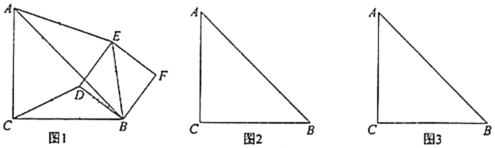
(1)发现:如图1,当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN与EC的位置关系是 ,MN与EC的数量关系是 .
(2)探究:若把(1)小题中的△AED绕点A顺时针旋转45°得到的图2,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
(3)若把(1)小题中的△AED绕点A逆时针旋转45°得到的图3,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
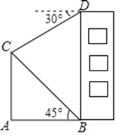
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com