
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

【答案】(1)①详见解析;②PA=PQ.(2)存在![]() ,使得②中的结论成立.
,使得②中的结论成立.
【解析】
(1)①如图1,作辅助线,构建等边三角形,证明△ADC为等边三角形.根据等边三角形三线合一可得∠PAC=∠PAD=30°;
②根据①中得结论:∠PAC=∠PQC=30°,则PA=PQ;
(2)存在k=![]() ,如图2,作辅助线,构建全等三角形,证明△PAD≌△PQC(SAS).可得结论.
,如图2,作辅助线,构建全等三角形,证明△PAD≌△PQC(SAS).可得结论.
解:(1)①如图1,在CM上取点D,使得CD=CA,连接AD,
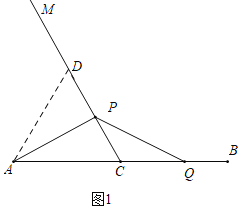
∵∠ACM=60°,
∴△ADC为等边三角形.
∴∠DAC=60°.
∵C为AB的中点,Q为BC的中点,
∴AC=BC=2BQ.
∵BQ=CP,
∴AC=BC=CD=2CP.
∴AP平分∠DAC.
∴∠PAC=∠PAD=30°.
②∵△ADC是等边三角形,
∴∠ACP=60°,
∵PC=CQ,
∴∠PQC=∠CPQ=30°,
∴∠PAC=∠PQC=30°,
∴PA=PQ;
(2)存在![]() ,使得②中的结论成立.
,使得②中的结论成立.
证明:过点P作PC的垂线交AC于点D.
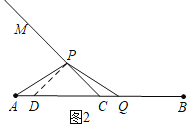
∵∠ACM=45°,
∴∠PDC=∠PCD=45°.
∴PC=PD,∠PDA=∠PCQ=135°.
∵![]() ,,
,,![]()
∴CD=BQ.
∵AC=BC,
∴AD=CQ.
∴△PAD≌△PQC(SAS).
∴PA=PQ.


科目:初中数学 来源: 题型:
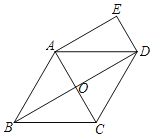
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
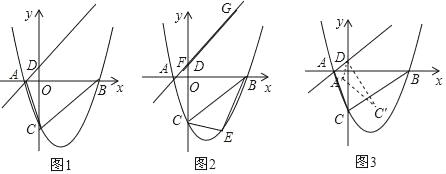
【题目】如图1,抛物线y=![]() x2﹣
x2﹣![]() x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为
x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为![]() ,直线AM与y轴交于点D,连接BC、AC.
,直线AM与y轴交于点D,连接BC、AC.
(1)求直线AD和BC的解折式;
(2)如图2,E为直线BC下方的抛物线上一点,当△BCE的面积最大时,一线段FG=4![]() (点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(3)如图3,将△DAC绕点D逆时针旋转角度α(0°<α<180°),记旋转中的三角形为△DA′C′,若直线A′C′分别与直线BC、y轴交于M、N,当△CMN是等腰三角形时,请直接写出CM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
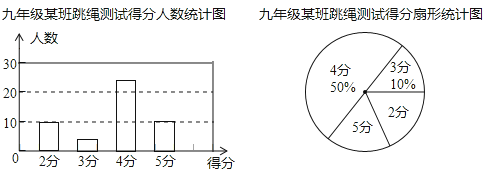
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是等圆,
是等圆,![]() 内接于
内接于![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.如图,
上.如图,
①以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
下面有四个结论:
①![]()
②![]()
③![]()
④![]()
所有正确结论的序号是( ).
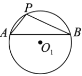
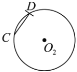
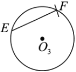
A.①②③④B.①②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
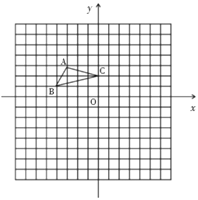
(1)直接写出![]() 关于原点
关于原点![]() 的中心对称图形
的中心对称图形![]() 各顶点坐标:
各顶点坐标:![]() ________
________![]() ________
________![]() ________;
________;
(2)将![]() 绕B点逆时针旋转
绕B点逆时针旋转![]() ,画出旋转后图形
,画出旋转后图形![]() .求
.求![]() 在旋转过程中所扫过的图形的面积和点
在旋转过程中所扫过的图形的面积和点![]() 经过的路径长.
经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量![]() ,这两个函数对应的函数值记为
,这两个函数对应的函数值记为![]() , 恒有点
, 恒有点![]() 和点
和点![]() 关于点
关于点![]() 成中心对称(此三个点可以重合),由于对称中心
成中心对称(此三个点可以重合),由于对称中心![]() 都在直线
都在直线![]() 上,所以称这两个函数为关于直线
上,所以称这两个函数为关于直线![]() 的“相依函数”。例如:
的“相依函数”。例如: ![]() 和
和![]() 为关于直线
为关于直线![]() 的 “相依函数”.
的 “相依函数”.
(1)已知点![]() 是直线
是直线![]() 上一点,请求出点
上一点,请求出点![]() 关于点
关于点![]() 成中心对称的点
成中心对称的点![]() 的坐标:
的坐标:
(2)若直线![]() 和它关于直线
和它关于直线![]() 的“相依函数”的图象与
的“相依函数”的图象与![]() 轴围成的三角形的面积为
轴围成的三角形的面积为![]() ,求
,求![]() 的值;
的值;
(3)若二次函数![]() 和
和![]() 为关于直线
为关于直线![]() 的“相依函数”.
的“相依函数”.
①请求出![]() 的值;
的值;
②已知点![]() 、点
、点![]() 连接
连接![]() 直接写出
直接写出![]() 和
和![]() 两条抛物线与线段
两条抛物线与线段![]() 有目只有两个交占时对应的
有目只有两个交占时对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com