
 双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°
双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°分析 (1)在Rt△ABC中,由三角函数求出BC的长度,得出CD即可;
(2)作FM⊥AB于M,则FM=BC=15$\sqrt{3}$米,在Rt△AMF中,AF=35米,由三角函数得出∠FAB>45°即可.
解答 解:(1)在Rt△ABC中,∠CAB=60°,
∴BC=AC•sin60°=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$≈15×1.73=25.95(米),
∴CD=BC+BD=25.95+1.5≈27.5(米);.
答:此时风筝离地面的高度约为27.5米;
(2)不能使∠FAB=45°;理由如下:
作FM⊥AB于M,如图所示:
则FM=BC=15$\sqrt{3}$米,
在Rt△AMF中,AF=35米,sin∠FAB=$\frac{FM}{AF}$=$\frac{15\sqrt{3}}{35}$≈0.7414>$\frac{\sqrt{2}}{2}$,
∴∠FAB>45°,
即小明站在原地不动时,风筝不能向右水平漂移到点F,使∠FAB=45°.
点评 本题考查了解直角三角形的应用、三角函数;由三角函数求出BC是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
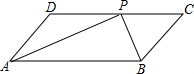 如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.
如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com