
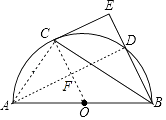
【题目】如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E. 
(1)求证:CE是半圆的切线;
(2)若OB=5,BC=8,求CE的长.
【答案】
(1)证明:如图,连接AD、OC,OC交AD于F.
∵ ![]() =
= ![]() ,
,
∴OC⊥AD,
∴AF=FD,∵OA=OB,
∴OF∥BD,即OC∥BE,
∵EC⊥EB,
∴EC⊥OC,
∴EC是⊙O的切线.
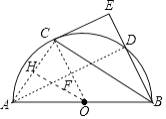
(2)解:连接AC,作OH⊥AC于H.
∵AB是直径,
∴∠ACB=90°,
∴AC= ![]() =
= ![]() =6,
=6,
∵OH⊥AC,
∴AH=CH=3,OH= ![]() =4,
=4,
∵S△AOC= ![]() ACOH=
ACOH= ![]() COAF,
COAF,
∴AF= ![]() =
= ![]() ,
,
∴DF=AF= ![]() ,
,
∵∠E=∠ECF=∠CFD=90°,
∴四边形ECFD是矩形,
∴EC=DF= ![]() .
.
【解析】(1)欲证明EC是⊙O的切线,只要证明EC⊥OC,只要证明OC∥EB即可.(2)连接AC,作OH⊥AC于H,在Rt△ABC中,利用勾股定理求出AC,再求出OH,利用S△AOC= ![]() ACOH=
ACOH= ![]() COAF求出AF,再证明CE=DF=AF即可解决问题.
COAF求出AF,再证明CE=DF=AF即可解决问题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料并解答下列问题.
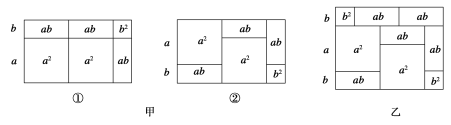
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE. 
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则 ![]() 的值是( )
的值是( ) 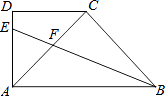
A.![]()
B.![]()
C.![]() +1
+1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)求证:△ABE≌△CAF
(2)如图①过A的直线与斜边BC不相交时,试探索EF、 BE、CF三条线段的关系;
(3)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求FE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯长25米,斜靠在一面墙上,梯子靠墙的一端距地面24米。(1)这个梯子底端离墙多少米?(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向也滑动了4米吗?如果不是,那滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:点A(0,0),B( ![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 . 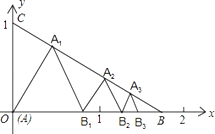
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com