
分析 设每天每个人传染x人,则第一天经过一个的传染共有(x+1)人得病,第二天(x+1)人每人传染x人,则共有(x+1)(x+1)人得病,此时为9人,可列方程求解x的解;再过两天,也就是第三天是(x+1)(x+1)人传染,和第四天(x+1)(x+1)(1+x)人传染,实际上共有(x+1)4人传染,由上次的结果代入即得.
解答 解:设每天平均一个人传染了x人,
则根据题意可列方程为:
(1+x)(1+x)=9,
解得:x1=2,x2=-4(舍去).
所以每天每人传播2人.
再经过2天的传染后,这个地区一共将会有(x+1)4=81人患甲型流感.
答:每天传染中平均一个人传染了2个人,再经过2天的传染后,这个地区一共将会有81人患甲型流感.
点评 本题考查的是一元二次方程的应用,每天每人传染的人数是一定的,新增加的病人与原先的老病人一起是成为新的传染源,这个要注意.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
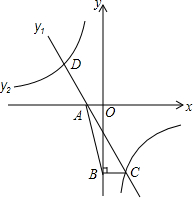 如图,直线y1=kx-$\frac{3}{2}$(k≠0)与双曲线y2=$\frac{m}{x}$交于点C、D,与x轴交于点A,
如图,直线y1=kx-$\frac{3}{2}$(k≠0)与双曲线y2=$\frac{m}{x}$交于点C、D,与x轴交于点A,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲超市与乙家超市一样 | B. | 甲超市比乙家超市便宜 | ||
| C. | 甲超市比乙家超市贵 | D. | 没有具体价格,无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(3x+2)=-3x+2 | B. | -(-2x-7)=-2x+7 | C. | -(5x-6)=6-5x | D. | -(-2x-7)=2x-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
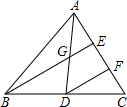 如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com