
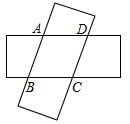
 如图,用完全相同的两个矩形纸片交叉叠合得到四边形ABCD,则四边形ABCD的形状是菱形.
如图,用完全相同的两个矩形纸片交叉叠合得到四边形ABCD,则四边形ABCD的形状是菱形. 分析 先根据长方形的两组对边分别平行,得出AB∥CD,BC∥AD,证出四边形ABCD为平行四边形;再作?ABCD的两条高AE、AF,由两张长方形纸条的宽度相等,得出AE=AF,根据平行四边形的面积不变,证出?ABCD有一组邻边相等;从而根据定义得出四边形ABCD为菱形.
解答 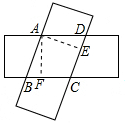 解:∵两张纸条都是长方形,
解:∵两张纸条都是长方形,
∴AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
过点A作AE⊥DC于E,AF⊥BC于F.
∵两张长方形纸条的宽度相等,
∴AE=AF.
又∵?ABCD的面积=DC•AE=BC•AF,
∴DC=BC,
∴?ABCD为菱形.
故答案是:菱形.
点评 本题主要考查学生对菱形判别方法的掌握;一个四边形为菱形的理论依据,常用三种方法:
①定义;②四边相等;③对角线互相垂直平分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题

| A. | 3.6米 | B. | 4.9米 | C. | 4.1米 | D. | 5.2米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2•n2=(mn)4 | B. | 5x2y-4x2y=1 | C. | m-2=$\frac{1}{{m}^{2}}$(m≠0) | D. | (m-n)2=m2-n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com