

分析 (1)根据已知得出PA=OA,然后根据三角形的面积就可求得P的坐标;
(2)根据已知求得M的坐标和三角形QPO的面积以及直线的解析式为y=-x+6,设此直线与x轴的交点为C,从而求得C的坐标,进而求得三角形QAC的面积,就可求得Q的纵坐标,代入直线y=-x+6,就可求得Q的坐标;
(3)分三种情况分析讨论求得.
解答  解:(1)如图1,∵P点在直线y=x上,
解:(1)如图1,∵P点在直线y=x上,
∴PA=OA,
∵S△PAO=$\frac{1}{2}$OA•PA=4.5.
∴OA=PA=3,
∴P(3,3);
故答案为(3,3);
(2)由于P(3,3),E(0,-1)
故PC的解析式为y=$\frac{4}{3}x-1$,
设PF的解析式为y=$-\frac{3}{4}x+b$,把P(3,3)代入求得b=$\frac{21}{4}$
,再令y=0,求得x=7
故F点坐标为(7,0).
(3)如图2,∵将点A向右平移5个单位长度得到点M,
∴M(8,0),
∴OM=8,
∵S△MPO=$\frac{1}{2}$OM•PA=$\frac{1}{2}×8$×3=12,S△QPO=S△MPO,
∴S△QPO=12,
∵Q为过点P的直线y=-x+a上一点,
∴3=-3+a,
∴a=6,
∴直线为y=-x+6,
∵直线y=x和直线y=-x+6垂直,
∴AC=OA=3,
∴OC=6,
∴S△OPC=$\frac{1}{2}$OC•PA=$\frac{1}{2}$×6×3=9,
∴S△OQC=12+9=21,
∴$\frac{1}{2}$OC•yQ=21,
∴yQ=7,
代入直线y=-x+6得7=-x+6,解得x=-1,
∴Q(-1,7);
(4)分三种情况:
当GH=O′G时,如图3,
∵∠PA′O′=45°,
∴∠PA′O′=∠GHO′=45°,
∴∠O′GH=90°,
∴PO′⊥x轴,
∴α=45°;
当GH=HO′时,如图4,∵∠PO′A′=45°,
∴∠PO′A′=∠HGO′=45°,
∴∠GHO′=90°,
∴A′O′⊥x轴,
∴α=90°;
当GO′=HO′时,如图5,∵∠PO′A′=45°,
∴∠GHO′=∠HGO′=65°,
∴∠PGA=65°,
∵∠PAG=90°,
∴∠APG=25°°,
∵∠OPA=45°,
∴α=70°,
∴当α为45°或70°或90°时,使△GHO′为等腰三角形.
点评 本题是一次函数的综合题,考查了一次函数图象上点的坐标特征,三角形的面积以及旋转的性质,分类讨论思想的运用是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
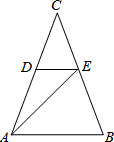 如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )| A. | 70° | B. | 65° | C. | 60° | D. | 55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com