

分析 (1)①如图1,根据等腰直角三角形的性质得到AB=AC,∠B=45°,EP=EQ,∠EPQ=45°,由三角形的内角和得到∠BDP=45°,推出∠PHD=90°,即可得到结论;②当点D经过点A时,△BPA为等腰直角三角形,根据勾股定理即可得到结论;
(2)如图2,连接ED,根据等腰直角三角形的性质得到ED⊥PQ,∠AED=∠PED=45°,ED=$\frac{1}{2}$PQ,推出△AED、△EBP与△PBQ都为等腰直角三角形,由勾股定理可得到AE=$\frac{\sqrt{2}}{2}$DE=$\frac{\sqrt{2}}{4}$PQ,BE=$\frac{\sqrt{2}}{2}$BP,列方程即可得到结论;
拓展:当4<t≤$\frac{16}{3}$时,如图3,根据三角形的面积公式即可得到结论;
探究:当点D在线段AB上时,求出QD=PD=t,PD=2t,过点A作AH⊥BC于点H,PH=BH-BP=4-t,在Rt△APH中求出AP的长度,(ⅰ)若AP=PQ,则有$\sqrt{{t}^{2}-8t+32}$=2t,(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,根据△PGQ∽△AHP求出PG的长度,(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,得出4=$\frac{1}{2}$×2t,求出方程的解即可;
解答 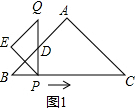 解:(1)①如图1,在等腰Rt△ABC中,AB=AC,∠B=45°,
解:(1)①如图1,在等腰Rt△ABC中,AB=AC,∠B=45°,
在等腰Rt△EPQ中,EP=EQ,∠EPQ=45°,
∵PD⊥BC,
∴∠BPD=90°,
∴∠BDP=45°,
∴∠PHD=90°,
∴PE⊥AB;
②在等腰Rt△BPD中,PB=PD,∠BPD=90°,
∴当点D经过点A时,△BPA为等腰直角三角形,
∴由勾股定理可得:PB=PA=$\frac{\sqrt{2}}{2}$BD=4,
∴t=$\frac{4}{1}$=4;
(2)如图2,连接ED,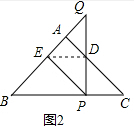
在等腰Rt△EPQ中,EQ=EP,D为PQ的中点,
∴ED⊥PQ,∠AED=∠PED=45°,ED=$\frac{1}{2}$PQ,
当E在AB边上时,△AED、△EBP与△PBQ都为等腰直角三角形,
∴由勾股定理可得:AE=$\frac{\sqrt{2}}{2}$DE=$\frac{\sqrt{2}}{4}$PQ,
BE=$\frac{\sqrt{2}}{2}$BP,
∵PQ=PB,
∴AE=$\frac{\sqrt{2}}{4}$PB
∴AB=AE+BE=$\frac{3\sqrt{2}}{4}$BP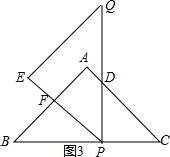
∵BP=t,
∴$\frac{3\sqrt{2}}{4}$t=4$4\sqrt{2}$
∴t=$\frac{16}{3}$;
∴当t是$\frac{16}{3}$时,点E在边AB上;
拓展:当4<t≤$\frac{16}{3}$时,如图3,
S=S△ABC-S△PBF-S△CPD=$\frac{1}{2}×$4$\sqrt{2}$×4$\sqrt{2}$-$\frac{1}{2}$t•$\frac{1}{2}$t-$\frac{1}{2}$×(8-t)2=-$\frac{3}{4}$t2+8t-16,
探究:存在,理由如下:
当点D在线段AB上时,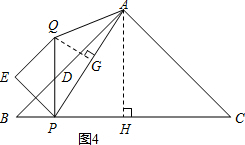
∵AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°-∠BAC)=45°.
∵PD⊥BC,
∴∠BPD=90°,
∴∠BDP=45°,
∴PD=BP=t,
∴QD=PD=t,
∴PQ=QD+PD=2t.
过点A作AH⊥BC于点H,
∵AB=AC,
∴BH=CH=$\frac{1}{2}$BC=4,AH=BH=4,
∴PH=BH-BP=4-t,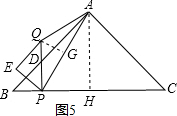
在Rt△APH中,AP=$\sqrt{A{H}^{2}+P{H}^{2}}$;
(ⅰ)若AP=PQ,则有$\sqrt{{t}^{2}-8t+32}$=2t.
解得:t1=$\frac{4\sqrt{7}-4}{3}$,t2=$\frac{-4\sqrt{7}-4}{3}$(不合题意,舍去);
(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,如图5,
∵∠BPQ=∠BHA=90°,
∴PQ∥AH.
∴∠APQ=∠PAH.
∵QG⊥AP,
∴∠PGQ=90°,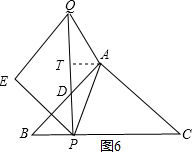
∴∠PGQ=∠AHP=90°,
∴△PGQ∽△AHP,
∴$\frac{PG}{AH}$=$\frac{PQ}{AP}$,即$\frac{PG}{4}$=$\frac{2t}{\sqrt{{t}^{2}-8t+32}}$,
∴PG=$\frac{8t}{\sqrt{{t}^{2}-8t+32}}$,
若AQ=PQ,由于QG⊥AP,则有AG=PG,即PG=$\frac{1}{2}$AP,
即$\frac{8t}{\sqrt{{t}^{2}-8t+32}}$=$\frac{1}{2}$$\sqrt{{t}^{2}-8t+32}$.
解得:t1=12-4$\sqrt{7}$,t2=12+4$\sqrt{7}$(不合题意,舍去);
(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,如图6,
易知四边形AHPT是矩形,故PT=AH=4.
若AP=AQ,由于AT⊥PQ,则有QT=PT,即PT=$\frac{1}{2}$PQ,
即4=$\frac{1}{2}$×2t.解得t=4.
当t=4时,A、P、Q三点共线,△APQ不存在,故t=4舍去.
综上所述,存在这样的t,使得△APQ成为等腰三角形,即t1=$\frac{4\sqrt{7}-4}{3}$,秒或t2=(12-4$\sqrt{7}$)秒.
点评 本题考查了三角形面积,相似三角形的性质和判定,三角形内角和定理,等腰直角三角形等知识点的综合运用,用了分类讨论思想和方程思想,难度偏大.


科目:初中数学 来源: 题型:解答题
 如图,一次函数$y=\frac{1}{2}x$的图象与反比例函数$y=\frac{k}{x}(k>0)$的图象交于A、B两点,AC⊥y轴,且S△AOC=16.
如图,一次函数$y=\frac{1}{2}x$的图象与反比例函数$y=\frac{k}{x}(k>0)$的图象交于A、B两点,AC⊥y轴,且S△AOC=16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
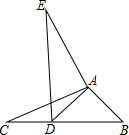 如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.
如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
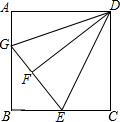 如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.
如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com