
 某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米).现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元?
某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米).现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元? 分析 连接AC,先证明△ACD是直角三角形,根据S四边形ABCD=S△BAC+S△DAC求出四边形ABCD的面积即可解决问题.
解答 解:连接AC,
∵∠B=90°,
∴在Rt△ABC中,AC2=AB2+BC=32+42=52,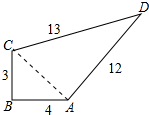
在△ACD中,CD2=132,AD2=122,
∵52+122=132,
∴AC2+AD2=CD2,
∴∠DAC=90°,
∴S四边形ABCD=S△BAC+S△DAC=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AC•AD=36cm2,
∵36×30=1080(元),
∴这块地全部种草的费用是1080元
点评 本题考查勾股定理以及勾股定理的逆定理的应用,解题的关键是证明△ADC是直角三角形,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线BD的长等于( )
如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线BD的长等于( )| A. | 6$\sqrt{3}$米 | B. | 6米 | C. | 3$\sqrt{3}$米 | D. | 3米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,已知直线y1=$-\frac{2}{3}$x+2与x轴、y轴分别交于点A和点B,直线y2=kx+b(k≠0)与x轴交于点C(1,0),且与线段AB相交于点P,并把△ABO分成两部分.
在平面直角坐标系中,已知直线y1=$-\frac{2}{3}$x+2与x轴、y轴分别交于点A和点B,直线y2=kx+b(k≠0)与x轴交于点C(1,0),且与线段AB相交于点P,并把△ABO分成两部分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )
如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )| A. | AG:AD=AE:AF | B. | AG:AD=EG:DF | C. | AG:AD=AE:AC | D. | AD:BC=DF:BE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD的周长为36cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于$\frac{9}{2}$cm.
如图,菱形ABCD的周长为36cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于$\frac{9}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )
如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )| A. | 16 | B. | 15.8 | C. | 15.6 | D. | 15.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.345×106 | B. | 3.45×105 | C. | 34.5×104 | D. | 345×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com