
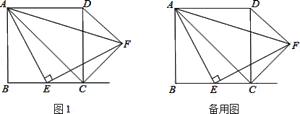
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求证:
,求证:
![]() ;
;
![]() ;
;
![]() 是等腰直角三角形.
是等腰直角三角形.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)取AB中点M,连接ME,利用正方形的性质和等腰直角三角形的性质,证明△AME△ECF,即可得出结论;
(2)利用(1)图,△AEF是等腰直角三角形,继而得到∠2=∠4、∠ACF=∠B,即可证得结论;
(3)过F分别作FN⊥BC的延长线于N,证得△FNE△EBA,得出△FCN是等腰直角三角形,易证四边形FNCP为矩形(正方形),求得∠FDC=∠DCF,得出结论.
![]() 如图
如图![]() ,
,

取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() 正方形边长,
正方形边长,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,即
,即![]() ,
,
∵![]() 为正方形
为正方形![]() 的对角线,
的对角线,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,
,

设正方形![]() 边长为
边长为![]() ,则
,则![]() ,
,![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
过![]() 作
作![]() 的延长线于
的延长线于![]() ,
,
则![]() ,
,
又由![]() 知,
知,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形(正方形),
为矩形(正方形),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
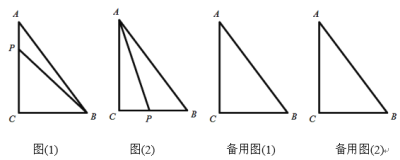
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,高AD和BE交于点H,∠ABC=45°,BE平分∠ABC,下列结论:①∠DAC= 22.5°;②BH= 2CE; ③若连结CH,则CH⊥AB;④若CD=1,则AH=2;其中正确的有( )
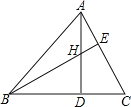
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com