
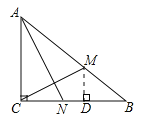
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.

【答案】(1)△BMN与△ABC相似时,t的值为![]() 或
或![]() ;(2)t=
;(2)t=![]()
【解析】试题分析:(1)由题意得出BM,CN, BN,BA,分两种情况讨论:①当△BMN∽△BAC时,利用相似三角形的性质得![]() ,解出t;②当△BMN∽△BCA时,
,解出t;②当△BMN∽△BCA时, ![]() ,解出t;
,解出t;
(2)过点M作MD⊥CB于点D,得到DM,BD,由BM=3tcm,CN=2tcm,得到CD,利用三角形相似的判定定理得△CAN∽△DCM,由三角形相似的性质得![]() ,解出t.
,解出t.
试题解析:(1)由题意知,BM=3tcm,CN=2tcm,∴BN=(8﹣2t)cm,BA=![]() =10(cm),当△BMN∽△BAC时,
=10(cm),当△BMN∽△BAC时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ;
;
当△BMN∽△BCA时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ,
,
∴△BMN与△ABC相似时,t的值为![]() 或
或![]() ;
;
(2)过点M作MD⊥CB于点D,由题意得:DM=BMsinB=![]() =
= ![]() (cm),BD=BMcosB=
(cm),BD=BMcosB=![]() =
= ![]() (cm),BM=3tcm,CN=2tcm,∴CD=(
(cm),BM=3tcm,CN=2tcm,∴CD=(![]() )cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴
)cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴![]() ,∴
,∴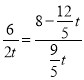 ,解得t=
,解得t=![]() .
.


科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,越来越多的家庭采取分户式采暖,降低采暖用气价格的呼声强烈.某市物价局对市区居民管道天然气阶梯价格制度的规定作出了调整,调整后的付款金额y(单位:元)与年用气量(单位:m3)之间的函数关系如图所示:
(1)宸宸家年用气量是270m3,求付款金额.
(2)皓皓家去年的付款金额是1300元,求去年的用气量.

查看答案和解析>>
科目:初中数学 来源: 题型:
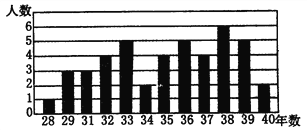
【题目】菲尔兹奖(The International Medals for Outstanding Discoveries in Mathematics)是国际数学联盟的国际数学家大会上颁发的奖项。每四年一次颁给有卓越贡献的年轻数学家,得奖者须在该年元旦前未满四十岁。菲尔兹奖被视为数学界的诺贝尔奖。本题中给出的条形图是截止到2002年44位费尔兹奖得主获奖时的年龄统计图。经计算菲尔兹奖得主获奖时的平均年龄是35岁。请根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时年龄的众数是多少?
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
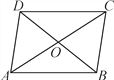
A. BO=DO B. CD=AB C. ∠BAD=∠BCD D. AC=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com