
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 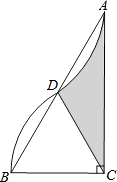
科目:初中数学 来源: 题型:
【题目】如图,沿AC方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=150°,沿BD的方向前进,取∠BDE=60°,测得BD=520m,BC=80m,并且AC,BD和DE在同一平面内,那么公路CE段的长度为( ) 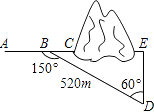
A.180m
B.260 ![]() m
m
C.(260 ![]() ﹣80)m
﹣80)m
D.(260 ![]() ﹣80)m
﹣80)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图B,E,C,F, 四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断 △ABC≌△DEF 的是 ( )
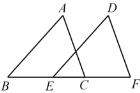
A. ∠A=∠D B. DF∥AC C. AC=DF D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,A是 ![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且 ![]() .
. 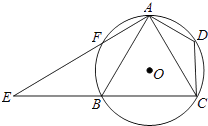
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费.如图是张磊家2018年1月和3月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度( )


A. 0.5元、0.6元 B. 0.4元、0.5元 C. 0.3元、0.4元 D. 0.6元、0.7元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一段长为1200m的笔直路上匀速跑步,甲、乙的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处.若同时起跑,甲、乙两人在从起跑至其中一人先到达终点的过程中,他们之间的距离y(m)与时间t(s)的函数图像如图所示.则t1=________s,y2=________m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
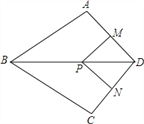
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com