
��μ�ʱ��������ͬѧ����һ��������Ϸ������������д�����֩�1��0��1�Ŀ�Ƭ�����DZ�����ȫ��ͬ���������ſ�Ƭ���泯��ϴ�Ⱥ�����һ��ͬѧ�����ȡһ�ţ����������������Ϊp��ֵ��Ȼ��Ƭ�Żز�ϴ�ȣ���һ��ͬѧ�ٴ������ſ�Ƭ�������ȡһ�ţ����������������Ϊqֵ�����ν����Ϊ��p��q����
��1���������������״ͼ���б�����ʾ��p��q�����п��ܳ��ֵĽ����
��2�����������x�ķ���x2+px+q=0û��ʵ����ĸ��ʣ�


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
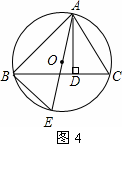
��ͼ4��AD�ǡ�ABC�ĸߣ�AE�ǡ�ABC�����Բ��O��ֱ������AB=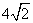 ��AC=5��AD=4�����O��ֱ��AE= ��
��AC=5��AD=4�����O��ֱ��AE= ��
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
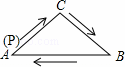
��ͼ���ڡ�ABC�У�AC=BC����һ����P�ӵ�A��������A��C��B��A�����˶�����CP�ij���s��ʱ��t֮��ĺ�����ϵ��ͼ�����������ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
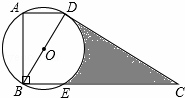
��ͼ����ֱ������ABCD�У���ABC=90�㣬�ϵ�ADΪ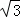 ���ԶԽ���BDΪֱ���ġ�O��CD���ڵ�D����BC���ڵ�E���ҡ�ABDΪ30�㣮��ͼ����Ӱ���ֵ����Ϊ��
���ԶԽ���BDΪֱ���ġ�O��CD���ڵ�D����BC���ڵ�E���ҡ�ABDΪ30�㣮��ͼ����Ӱ���ֵ����Ϊ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x�ύ�ڵ�A����4��0����B����1��0�����㣮
��1���������ߵĽ���ʽ��
��2���ڵ�����������������һ����D��
����ͼ��1�������ı���ODAE����OAΪ�Խ��ߵ�ƽ���ı��Σ���ƽ���ı���ODAE�����Ϊ6ʱ�����ж�ƽ���ı���ODAE�Ƿ�Ϊ���Σ�˵�����ɣ�
����ͼ��2����ֱ��y=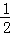 x+3�������߽��ڵ�Q��C���㣬����D��ֱ��DF��x���ڵ�H����QC�ڵ�F�������Ƿ���������ĵ�D��ʹ��D��ֱ��CQ�ľ������C��ֱ��DF�ľ���֮��Ϊ
x+3�������߽��ڵ�Q��C���㣬����D��ֱ��DF��x���ڵ�H����QC�ڵ�F�������Ƿ���������ĵ�D��ʹ��D��ֱ��CQ�ľ������C��ֱ��DF�ľ���֮��Ϊ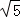 ��2�������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��2�������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ�˽�ijС��С����ٵ�ѧϰ���������ʦ��������˸�С��8��С��ij���ѧϰʱ�䣬������£���λ��Сʱ����1.5 ��1.5 ��3 ��4��2 ��5 ��2.5 ��4.5.�����������ݣ����н�����������
A. ������3.5 B. ������1.5 C. ��λ����3 D.ƽ������3


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����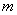 ��
��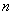 �Σ�ƽ������
�Σ�ƽ������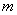 ��
��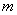 ��
��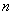 ��
��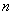 ��֮��ľ���ֱ�Ϊ
��֮��ľ���ֱ�Ϊ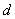 1��
1��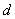 2��
2��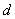 3����
3����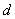 1 =
1 =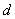 3 = 1��
3 = 1��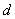 2 = 2 . ���ǰ��ĸ�����ֱ��ڡ�
2 = 2 . ���ǰ��ĸ�����ֱ��ڡ�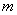 ��
��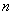 ��������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ�.
��������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ�.
��̽��1�� �� ��ͼ1��������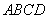 Ϊ�������ı��Ρ���
Ϊ�������ı��Ρ���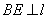 �ڵ�
�ڵ�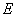 ,
,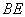 �ķ����ӳ��߽�ֱ���ڵ�
�ķ����ӳ��߽�ֱ���ڵ� . ��������
. ��������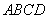 �ı߳�.
�ı߳�.
��̽��2�� �� ����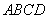 Ϊ�������ı��Ρ����䳤 ���� = 2 ��1 �������
Ϊ�������ı��Ρ����䳤 ���� = 2 ��1 �������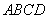 �Ŀ�Ϊ_____. (ֱ��д���������)
�Ŀ�Ϊ_____. (ֱ��д���������)
��̽��3�� �� ��ͼ2������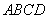 Ϊ�������ı��Ρ��ҡ�
Ϊ�������ı��Ρ��ҡ�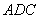 =60�㣬��
=60�㣬��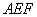 �ǵȱ������Σ�
�ǵȱ������Σ�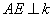 �ڵ�
�ڵ�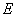 �� ��
�� ��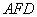 =90�㣬ֱ��
=90�㣬ֱ��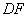 �ֱ�ֱ�ߡ��ڵ�
�ֱ�ֱ�ߡ��ڵ� ��
��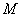 . ��֤��
. ��֤��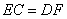 .
.
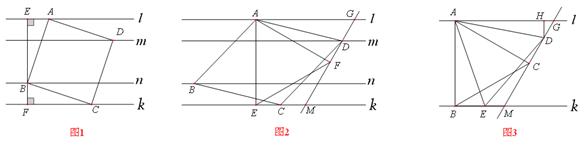
���� չ�� �� ��ͼ3���Σ��ȱ�������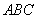 �Ķ���
�Ķ���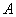 ��
��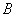 �ֱ�����ֱ�ߡ��ϣ�
�ֱ�����ֱ�ߡ��ϣ�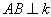 �ڵ�
�ڵ�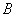 �� ��
�� ��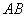 =4 ����
=4 ����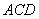 =90�㣬ֱ��
=90�㣬ֱ��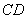 �ֱ�ֱ�ߡ��ڵ�
�ֱ�ֱ�ߡ��ڵ� ��
��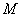 ����
����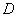 ��
��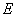 �ֱ����߶�
�ֱ����߶�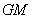 ��
��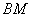 �ϵĶ��㣬��ʼ�ձ���
�ϵĶ��㣬��ʼ�ձ��� =
=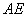 ��
��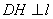 �ڵ�
�ڵ�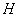 .
.
���룺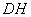 ��ʲô��Χ�ڣ�
��ʲô��Χ�ڣ�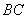 ��
��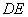 ����˵����ʱ
����˵����ʱ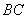 ��
��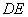 ������.
������.
 |


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com