
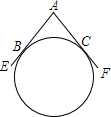
 一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.
一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径. 分析 连接OB、OC、AO,可证三角形OBC是等边,从而测量BC即可,∠AOC=30°,$OC=\sqrt{3}AC$,从而测量AC即可.
解答 解:方法一:
测量BC的长度即为半径,2BC即为直径,原因如下:
设圆心为O,连接OB、OC,则OB⊥AB,OC⊥AC,如图1,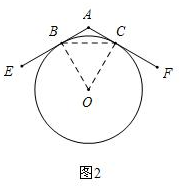
∵∠A=120°,
∴∠BOC=60°,
∴△BOC为等边三角形,
∴BC=OB=OC.
方法二:
测量AC的长度,再乘以$\sqrt{3}$即可,原因如下: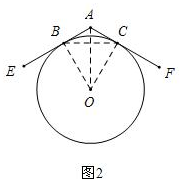
在方法一的基础上,连接AO,则∠AOC=30°,$OC=\sqrt{3}AC$.
点评 本题主要考查了圆的切线性质、特殊角的三角函数、等腰三角形性质、等边三角形的判定、四边形内角和性质等知识点,难度适中.本题以设计题的方式考查学生将所学几何知识用于解决实际问题的能力,解答过程充分体现了化归与转化的数学思想.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com