
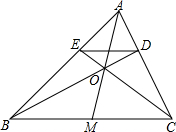
 已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC.
已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC. 分析 根据三角形面积公式易得S△ABD=S△ACD,S△BOD=S△COD,把它们相减即可得到S△ABO=S△ACO,再计算$\frac{AE}{BE}$=$\frac{{S}_{△ACE}}{{S}_{△BCE}}$=$\frac{{S}_{△AOE}}{{S}_{△BOE}}$=$\frac{{S}_{△ACE}-{S}_{△AOE}}{{S}_{△BCE}{-S}_{△BOE}}$=$\frac{{S}_{△AOC}}{{S}_{△BOC}}$,同理可得$\frac{AD}{CD}$=$\frac{{S}_{△AOB}}{{S}_{△BOC}}$,$\frac{AE}{BE}$=$\frac{AD}{CD}$,然后根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边得到结论.
解答 证明:∵AM是边BC的中线,
∴BM=CM,
∴S△ABM=S△ACM,S△BOM=S△COM,
∴S△ABO=S△ACO,
∵$\frac{AE}{BE}$=$\frac{{S}_{△ACE}}{{S}_{△BCE}}$=$\frac{{S}_{△AOE}}{{S}_{△BOE}}$=$\frac{{S}_{△ACE}-{S}_{△AOE}}{{S}_{△BCE}{-S}_{△BOE}}$=$\frac{{S}_{△AOC}}{{S}_{△BOC}}$,
同理可得$\frac{AD}{CD}$=$\frac{{S}_{△AOB}}{{S}_{△BOC}}$,
∴$\frac{AE}{BE}$=$\frac{AD}{CD}$,
∴ED∥BC.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)
如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
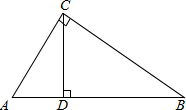 如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.
某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com