
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
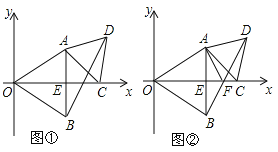
【题目】如图,△AOB和△ACD是等边三角形,其中AB⊥x轴于E点,点E坐标为(3,0),点C(5,0).
(1)如图①,求BD的长;
(2)如图②,设BD交x轴于F点,求证:∠OFA=∠DFA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
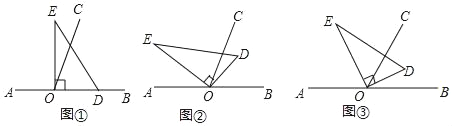
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
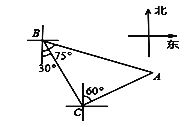
【题目】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.50B.25C.25![]() D.25
D.25![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字:
对于(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
可以如下计算:
原式=[(﹣5)+(﹣![]() )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣![]() )]+(17+
)]+(17+![]() )+[(﹣3)+(﹣
)+[(﹣3)+(﹣![]() )]
)]
=[(一5)+(﹣9)+17+(一3)]+[(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() +(﹣
+(﹣![]() )]=0+(﹣1
)]=0+(﹣1![]() )
)
=﹣1![]()
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1![]() )+(﹣2000
)+(﹣2000![]() )+4000
)+4000![]() +(﹣1999
+(﹣1999![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,点E是边AB的中点,延长DE交CB的延长线于点F.
中,点E是边AB的中点,延长DE交CB的延长线于点F.
(1)求证:![]() ;
;
(2)若![]() ,连接EC,则
,连接EC,则![]() 的度数是__________________
的度数是__________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com