
【题目】某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的 ![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
【答案】
(1)解:设A型每套x元,则B型每套(x+40)元.
由题意得:4x+5(x+40)=1820.
解得:x=180,x+40=220.
即购买一套A型课桌凳和一套B型课桌凳各需180元、220元
(2)解:设购买A型课桌凳a套,则购买B型课桌凳(200﹣a)套.
由题意得:  ,
,
解得:78≤a≤80.
∵a为整数,
∴a=78、79、80.
∴共有3种方案,
设购买课桌凳总费用为y元,
则y=180a+220(200﹣a)=﹣40a+44000.
∵﹣40<0,y随a的增大而减小,
∴当a=80时,总费用最低,此时200﹣a=120,
即总费用最低的方案是:购买A型80套,购买B型120套
【解析】(1)根据购买一套A型课桌凳比购买一套B型课桌凳少用40元,以及购买4套A型和5套B型课桌凳共需1820元,得出等式方程求出即可;(2)利用要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的 ![]() ,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.


科目:初中数学 来源: 题型:
【题目】在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
![]() 求购买1个篮球和1个足球各需多少元?
求购买1个篮球和1个足球各需多少元?
![]() 若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC.

(1)过A作AE⊥BC,过B作BF⊥AC,垂足分别为E,F,AE,BF相交于H;
(2)过A作AM∥BC,过B作BM∥AC,相交于M;
(3)若∠AMB=115°,求∠AHB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的周长是20,三边分别为a,b,c.
(1)若b是最大边,求b的取值范围;
(2)若△ABC是三边均不相等的三角形,b是最大边,c是最小边,且b=3c,a,b,c均为整数,求△ABC的三边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
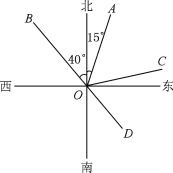
【题目】如图,射线OA表示的方向是北偏东15°,射线OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,则射线OC表示的方向是 ;
(2)若射线OD是射线OB的反向延长线,则射线OD表示的方向是 ;
(3)∠BOD可以看作是由OB绕点O逆时针方向旋转至OD形成的角,作∠BOD的平分线OE;
(4)在(1),(2),(3)的条件下,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将探究过程补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ![]() ;
;
(1)构造函数,画出图象 设y3=x2+4x﹣1,y4= ![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(3)借助图象,写出解集 结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com