练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】能使6|k+2|＝（k+2）2成立的k值为_____．

    【答案】﹣2，4或﹣8

    【解析】

    根据解方程的方法可以求得6|k+2|＝（k+2）2成立的k的值，本题得以解决．

    解：6|k+2|＝（k+2）2

    6|k+2|﹣|k+2|2＝0，

    ∴|k+2|（6﹣|k+2|）＝0，

    ∴|k+2|＝0或6﹣|k+2|＝0，

    解得，k＝﹣2，k＝4或k＝﹣8，

    故答案为：﹣2，4或﹣8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】分解因式x3y﹣6x2y+9xy＝_______________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是（　　）

    A. 25° B. 30° C. 35° D. 40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是中国古代的数学专著，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三．问人数、羊价各几何？”译文：“假设有若干人共同出钱买羊，如果每人出5钱，那么还差45钱；如果每人出7钱那么仍旧差3钱，求买羊的人数和羊的价钱．”设共有x个人买羊，可列方程为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一平面内，的两条直线叫做平行线．若直线与直线平行， 则记作 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小红和小明在研究一个数学问题：已知AB∥CD，AB和CD都不经过点E，探索∠E与∠A，∠C的数量关系．
    （1）发现：在图1中，小红和小明都发现：∠AEC=∠A+∠C； 小红是这样证明的：如图7过点E作EQ∥AB．
    ∴∠AEQ=∠A（）
    ∵EQ∥AB，AB∥CD．
    ∴EQ∥CD（）
    ∴∠CEQ=∠C
    ∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C．
    小明是这样证明的：如图7过点E作EQ∥AB∥CD．
    ∴∠AEQ=∠A，∠CEQ=∠C
    ∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
    请在上面证明过程的横线上，填写依据：
    两人的证明过程中，完全正确的是 ．
    （2）尝试： ①在图2中，若∠A=110°，∠C=130°，则∠E的度数为；
    ②在图3中，若∠A=20°，∠C=50°，则∠E的度数为 ．
    （3）探索： 装置图4中，探索∠E与∠A，∠C的数量关系，并说明理由．
    （4）猜想： 如图5，∠B、∠D、∠E、∠F、∠G之间有什么关系？（直接写出结论）
    （5）如图6，你可以得到什么结论？（直接写出结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3 ， …组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 个单位长度，则第2017秒时，点P的坐标是（ ）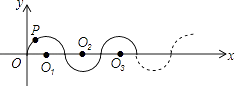

    A.（2016，0）
    B.（2017，1）
    C.（2017，﹣1）
    D.（2018，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店需要购进甲、乙两种商品共180件，其进价和售价如表：（注：获利=售价﹣进价）

    甲

    乙

    进价（元/件）

    14

    35

    售价（元/件）

    20

    43


    （1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
    （2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某体育用品商店为了解5月份的销售情况，对本月各类商品的销售情况进行调查，并将调查的结果绘制成如下两幅不完整的统计图

    （1）请根据图中提供的信息，将条形图补充完整；

    （2）该商店准备按5月份球类商品销量的数量购进球类商品，含篮球、足球、排球三种球，预计恰好用完进货款共3600元，设购进篮球x个，足球y个，三种球的进价和售价如表：

    类别

    篮球

    足球

    排球

    进价（单位：元/个）

    50

    30

    20

    预售价（单位：元/个）

    70

    45

    25

    求出y与x之间的函数关系式；

    （3）在（2）中的进价和售价的条件下，据实际情况，预计足球销售超过60个后，这种球就会产生滞销

    ①假设所购进篮球、足球、排球能全部售出，求出预估利润P（元）与x（个）的函数关系式；

    ②求出预估利润的最大值，并写出此时购进三种球各多少个．

    查看答案和解析>>

    同步练习册答案