
【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.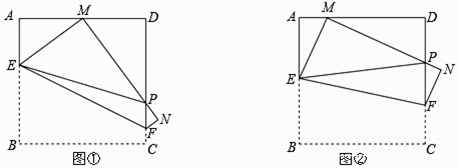
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
【答案】
(1)
解:①依据翻折的性质可知∠EMP=∠B=90°,∠C=∠N=90°
∴∠AME+∠PMD=90°.
又∵∠AME+∠AEM=90°,
∴∠AEM=∠PMD.
又∵∠A=∠D,
∴△AME∽△DPM.
∵∠MPD=∠FPN,∠D=∠N=90°
∴△MPD∽△FPN.
∵△AME∽△DPM,
∴ ![]() .
.
又∵AM=MD,
∴ ![]() .
.
又∵∠EMP=∠D=90°,
∴△EMP∽△MDP.
所以有:△AME∽△DPM,△AME∽△DPM,△EMP∽△MDP.
②∵四边形ABCD是正方形,
∴AD=AB=4.
∵点M是AD边中点,
∴AM=DM=2.
由折叠的性质得:ME=BE,
∴△MEA的周长为6.
在Rt△MEA中,设AE=x,则ME=4﹣x.
∴x2+22=(4﹣x)2,解得:x= ![]() .
.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() .
.
∴△PMD的周长为8
(2)
解:△PMD的周长不变.
设AM=m,AE=n,则DM=4﹣m,EM=4﹣n,△AEM的周长=4+m.
在Rt△AME中,依据勾股定理可知:m2+n2=(4﹣n)2,即8n=16﹣m2.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() .
.
∴△PMD的周长= ![]() =
= ![]() =
= ![]() =8
=8
【解析】(1)①依据两组角对应相等的三角形相似可证明△AEM∽△DMP,△PFN∽△PMD,然后依据两组边对应成比例且夹角相等的两个三角形相似证明△EMP∽△MDP即可;②设AE=x,则EM=4﹣x,在Rt△AEM中,依据勾股定理可求得x的值,然后可求得△AEM的周长,然后依据相似三角形的周长比等于相似比求解即可;(2)设AM=m,AE=n,则DM=4﹣m,EM=4﹣n.在Rt△AEM中,依据勾股定理和完全平方公式可得到8n=16﹣m2 , 然后可△PMD∽△MEA可求得△PMD的周长.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)和相似三角形的应用的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(3a2-ab+7)-(5ab-4a2+7),其中, a=2,b=![]() ;
;
(2)3(ab-5b2+2a2)-(7ab+16a2-25b2),其中|a-1|+(b+1)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一张长方形纸条上画一条数轴.
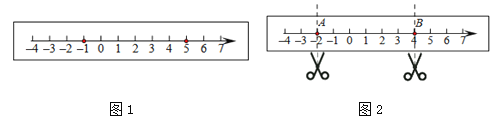
(1)折叠纸条使数轴上表示![]() 的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
(2)如果数轴上两点之间的距离为8,经过(1)的折叠方式能够重合,那么左边这个点表示的数是 ;
(3)如图2,点A、B表示的数分别是![]() 、
、![]() ,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折![]() 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含
次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
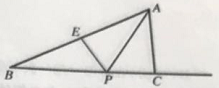
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,E为斜边AB的中点,点P是射线BC的一个动点,连接AP、PE,将△AEP沿着边PE叠,折叠后得到△EPA,当折叠后△EPA与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则BP的长__________
查看答案和解析>>
科目:初中数学 来源: 题型:
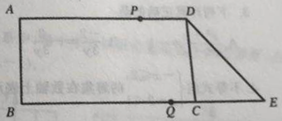
【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)求DE的长
(2)当t为多少时,四边形PQED成为平行四边形;
(3)请直接写出使得△DQE是等腰三角形时t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.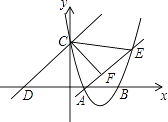
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com