��1����y=0�����x
1=-1��x
2=3
��A��-1��0��B��3��0��
��C������x=2����y=x
2-2x-3��y=-3
��C��2��-3��
��ֱ��AC�ĺ�������ʽ��y=-x-1��
��2����P��ĺ�����Ϊx��-1��x��2��
��P��E������ֱ�Ϊ��P��x��-x-1��
E��x��x
2-2x-3��
��P����E����Ϸ���PE=��-x-1��-��x
2-2x-3��=-x
2+x+2=-��x-
��
2+
��
�൱
x=ʱ��PE�����ֵ=
��
��3������4�������ĵ�F���ֱ���F
1��1��0����F
2��-3��0����F
3��4+
��0����F
4��4-
��0����
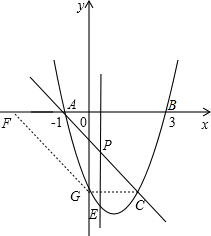
����ͼ������C�������ߺ�y��Ľ��㣬��ôCG
��x�ᣬ��ʱAF=CG=2�����F��������ǣ�-3��0����
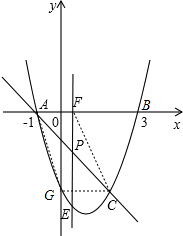
����ͼ��AF=CG=2��A�������Ϊ��-1��0�������F�������Ϊ��1��0����
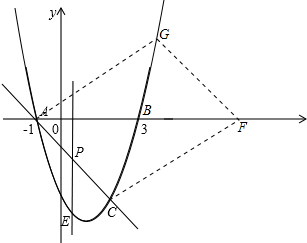
����ͼ����ʱC��G��������������x��Գƣ����G���������Ϊ3�������������м��ɵó�G�������Ϊ��1+
��3��������ֱ��GF��б����ֱ��AC����ͬ����˿���ֱ��GF�Ľ���ʽΪy=-x+h����G������ɵó�ֱ�ߵĽ���ʽΪy=-x+4+
�����ֱ��GF��x��Ľ���F������Ϊ��4+
��0����
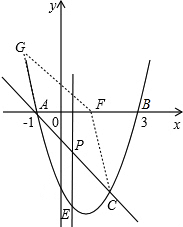
����ͼ��ͬ�ۿ����F������Ϊ��4-
��0����
�ۺ���������ɵó�������4������������F�㣮








 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�