
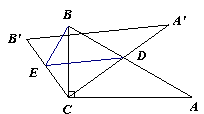
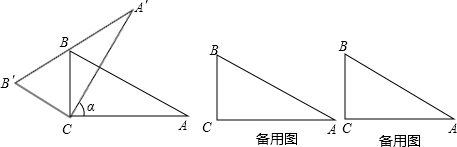
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ),得到Rt△
),得到Rt△![]() .
.
(1)如图,当边![]() 经过点B时,求旋
经过点B时,求旋![]() 转角
转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥![]()
交![]() 边于点E,联结BE.
边于点E,联结BE.
① 当![]() 时,设AD=
时,设AD=![]() ,BE=
,BE=![]() ,求
,求![]() 与
与![]() 之间的函数解析式及自变量
之间的函数解析式及自变量![]() 的取值范围;
的取值范围;
② 当![]() 时,求AD的长.
时,求AD的长.

(1)在Rt△![]() 中,∵∠A=30°,∴
中,∵∠A=30°,∴![]() .
.![]() ………………………1分
………………………1分
由旋转可知:![]() ,
,![]() ,
,![]()
 ∴△
∴△![]() 为等边三角形.……………2分
为等边三角形.……………2分
∴![]() =
=![]() . ……………3分
. ……………3分
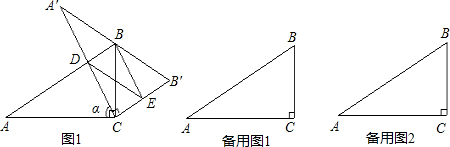
(2)① 当![]() 时,点D在AB边上(如图).
时,点D在AB边上(如图).
∵ DE∥![]() , ∴
, ∴ ![]() .
.
由旋转性质可知,CA =![]() ,CB=
,CB=![]() , ∠ACD=∠BCE.
, ∠ACD=∠BCE.
∴ ![]() ∴
∴ ![]() .
.
∴ △CAD∽△CBE. ………………………………………………6分
∴![]() .∵∠A=30° ∴
.∵∠A=30° ∴![]()
![]() .
.
∴![]() (0﹤
(0﹤![]() ﹤2) ………………………………………………8分
﹤2) ………………………………………………8分
②当![]() 时,点D在AB边上
时,点D在AB边上
AD=x,![]() ,∠DBE=90°.
,∠DBE=90°.
此时,![]() .
.
当S =![]() 时,
时,![]() .整理,得
.整理,得 ![]() .
.
解得 ![]() ,即AD=1. ………………………………………………10分
,即AD=1. ………………………………………………10分
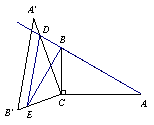
当![]() 时,点D在AB的延长线上(如图
时,点D在AB的延长线上(如图![]() ).
).
仍设AD=x,则![]() ,∠DBE=90°.
,∠DBE=90°.
![]() .
.
当S =![]() 时,
时,![]() .
.
整理,得 ![]() .
.
解得 ![]() ,
,![]() (负值,舍去).
(负值,舍去).
即![]() . ………………………………………………12分
. ………………………………………………12分
综上所述:AD=1或![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
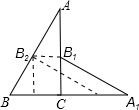 如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )
如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )A、(3π+3-
| ||||
B、(3π-3+
| ||||
C、(
| ||||
D、(
|
查看答案和解析>>
科目:初中数学 来源: 题型:
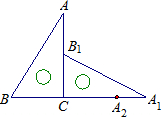 如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是
如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com