
ЁОЬтФПЁПФГжабЇОйааИжБЪЪщЗЈДѓШќЃЌЖдИїФъМЖЭЌбЇЕФЛёНБЧщПіНјааСЫЭГМЦЃЌВЂЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
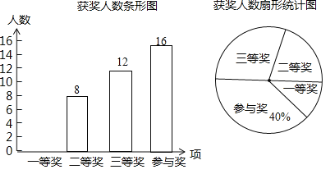
ЧыНсКЯЭМжаЯрЙиаХЯЂНтД№ЯТСаЮЪЬтЃК
(1)ЩШаЮЭГМЦЭМжаШ§ЕШНБЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ______ЖШЃЛ
(2)ЧыНЋЬѕаЮЭГМЦЭМВЙШЋЃЛ
(3)ЛёЕУвЛЕШНБЕФЭЌбЇжага![]() РДздЦпФъМЖЃЌга
РДздЦпФъМЖЃЌга![]() РДздОХФъМЖЃЌЦфЫћЭЌбЇОљРДздАЫФъМЖЃЎЯжзМБИДгЛёЕУвЛЕШНБЕФЭЌбЇжаШЮбЁ2ШЫВЮМгЪаМЖИжБЪЪщЗЈДѓШќЃЌЧыЭЈЙ§СаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЫљбЁГіЕФ2ШЫжаМШгаАЫФъМЖЭЌбЇгжгаОХФъМЖЭЌбЇЕФИХТЪЃЎ
РДздОХФъМЖЃЌЦфЫћЭЌбЇОљРДздАЫФъМЖЃЎЯжзМБИДгЛёЕУвЛЕШНБЕФЭЌбЇжаШЮбЁ2ШЫВЮМгЪаМЖИжБЪЪщЗЈДѓШќЃЌЧыЭЈЙ§СаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЫљбЁГіЕФ2ШЫжаМШгаАЫФъМЖЭЌбЇгжгаОХФъМЖЭЌбЇЕФИХТЪЃЎ
ЁОД№АИЁП(1)108ЃЛ(2)ВЙЭММћНтЮіЃЛ(3)![]() .
.
ЁОНтЮіЁП
(1)ЯШИљОнВЮгыНБЕФШЫЪ§МАЦфЫљеМАйЗжБШЧѓЕУзмШЫЪ§ЃЌдйгУ![]() ГЫвдШ§ЕШНБШЫЪ§ЫљеМБШР§МДПЩЕУД№АИЃЛ(2)ИљОнзмШЫЪ§ЧѓГівЛЕШНБЕФШЫЪ§ЃЌВЙШЋЭМаЮМДПЩЃЛ(3)ЛЪїзДЭМЕУГіЫљгаЕШПЩФмНсЙћЃЌдйДгжаевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌРћгУИХТЪЙЋЪНМЦЫуМДПЩЕУД№АИЃЎ
ГЫвдШ§ЕШНБШЫЪ§ЫљеМБШР§МДПЩЕУД№АИЃЛ(2)ИљОнзмШЫЪ§ЧѓГівЛЕШНБЕФШЫЪ§ЃЌВЙШЋЭМаЮМДПЩЃЛ(3)ЛЪїзДЭМЕУГіЫљгаЕШПЩФмНсЙћЃЌдйДгжаевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌРћгУИХТЪЙЋЪНМЦЫуМДПЩЕУД№АИЃЎ
(1)ЁпБЛЕїВщЕФзмШЫЪ§ЮЊ![]() (ШЫ)ЃЌ
(ШЫ)ЃЌ
ЁрЩШаЮЭГМЦЭМжаШ§ЕШНБЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК108ЃЛ
(2)вЛЕШНБШЫЪ§ЮЊ![]() (ШЫ)ЃЌ
(ШЫ)ЃЌ
ВЙШЋЭМаЮШчЯТЃК
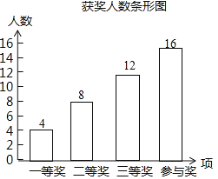
(3)вЛЕШНБжаЃЌЦпФъМЖШЫЪ§ЮЊ![]() (ШЫ)ЃЌОХФъМЖШЫЪ§ЮЊ
(ШЫ)ЃЌОХФъМЖШЫЪ§ЮЊ![]() (ШЫ)ЃЌдђАЫФъМЖЕФга2ШЫЃЌ
(ШЫ)ЃЌдђАЫФъМЖЕФга2ШЫЃЌ
ЛЪїзДЭМШчЯТЃК
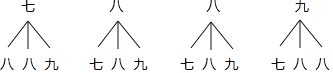
гЩЪїзДЭМжЊЃЌЙВга12жжЕШПЩФмНсЙћЃЌЦфжаЫљбЁГіЕФ2ШЫжаМШгаАЫФъМЖЭЌбЇгжгаОХФъМЖЭЌбЇЕФга4жжНсЙћЃЌ
ЫљвдЫљбЁГіЕФ2ШЫжаМШгаАЫФъМЖЭЌбЇгжгаОХФъМЖЭЌбЇЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЎНЋ
ЃЎНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊ
ЫГЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊ![]() ЃЎ
ЃЎ
Ђй Ђк
Ђк
Ђл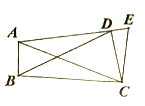 Ђм
Ђм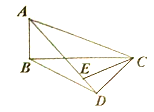
ЃЈ1ЃЉЮЪЬтЗЂЯжЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЭиеЙЬНОПЃКЪдХаЖЯЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМЂкЕФЧщПіИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМЂкЕФЧщПіИјГіжЄУїЃЎ
ЃЈ3ЃЉЮЪЬтНтОіЃКЕБ![]() а§зЊжС
а§зЊжС![]() Ш§ЕуЙВЯпЪБЃЌШчЭМЂлЃЌЭМЂмЃЌжБНгаДГіЯпЖЮ
Ш§ЕуЙВЯпЪБЃЌШчЭМЂлЃЌЭМЂмЃЌжБНгаДГіЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЮЊЖўДЮКЏЪ§ЭМЯѓЩЯШЮвЛЕуЃЎ
ЮЊЖўДЮКЏЪ§ЭМЯѓЩЯШЮвЛЕуЃЎ
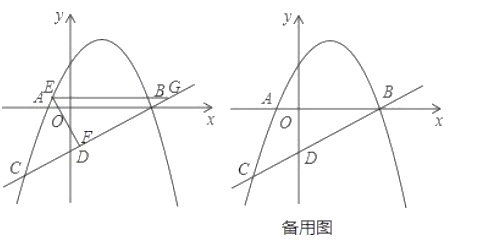
![]() ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
![]() ШєЕу
ШєЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§
ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§![]() ЗжБ№зї
ЗжБ№зї![]() КЭ
КЭ![]() жсЕФДЙЯпЃЌНЛжБЯп
жсЕФДЙЯпЃЌНЛжБЯп![]() гкВЛЭЌЕФСНЕу
гкВЛЭЌЕФСНЕу![]() дк
дк![]() ЕФзѓВр)ЃЌЧѓ
ЕФзѓВр)ЃЌЧѓ![]() жмГЄЕФзюДѓжЕЃЛ
жмГЄЕФзюДѓжЕЃЛ
![]() ЪЧЗёДцдкЕу
ЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧвд
ЪЧвд![]() ЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧѓЕу
ЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧѓЕу![]() ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
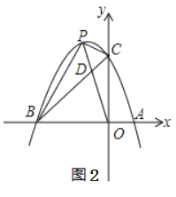
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2ЃЋbxЃЋ3ОЙ§ЕуA ЃЈ1ЃЌ0ЃЉКЭЕуB ЃЈЃ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌЕуPЮЊЕкЖўЯѓЯоФкХзЮяЯпЩЯЕФЖЏЕуЃЎ
ЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊ__________ЃЌХзЮяЯпЕФЯюЕузјБъЮЊ__________ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮBOCPЕФУцЛ§ЮЊ8?ШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгOPНЛBCгкЕуDЃЌЕБSЁїCPDЁУSЁїBPDЃН1ЁУ2ЪБЃЌЧыЧѓГіЕуDЕФзјБъЃЛ
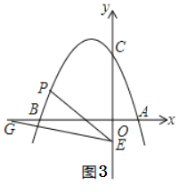
ЃЈ4ЃЉШчЭМ3ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌЃ1ЃЉЃЌЕуGЮЊxжсИКАыжсЩЯЕФвЛЕуЃЌЁЯOGEЃН15ЁуЃЌСЌНгPEЃЌШєЁЯPEGЃН2ЁЯOGEЃЌЧыЧѓГіЕуPЕФзјБъЃЎ
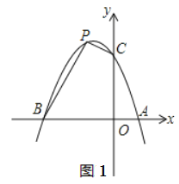
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1,дк![]() жа,
жа,![]() ,
,![]() ,Еу
,Еу![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕу,СЌНг
ЕФжаЕу,СЌНг![]() .
.
(1)ЬНЫїЗЂЯж:

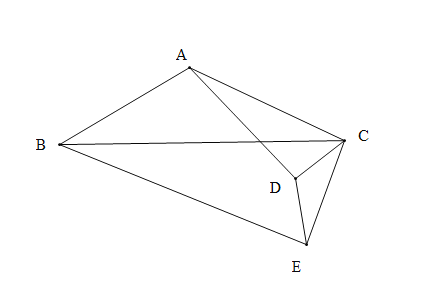
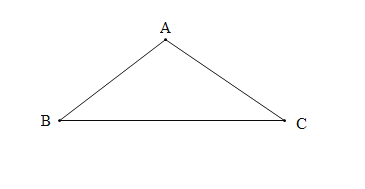
ЭМ1жа,![]() ЕФжЕЮЊ_____________;
ЕФжЕЮЊ_____________;![]() ЕФжЕЮЊ_________ЃЎ
ЕФжЕЮЊ_________ЃЎ
(2)ЭиеЙЬНОП
ШєНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыЗНЯђа§зЊвЛжм,дка§зЊЙ§ГЬжа
ФцЪБеыЗНЯђа§зЊвЛжм,дка§зЊЙ§ГЬжа![]() ЕФДѓаЁгаЮоБфЛЏ?ЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏ?ЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
(3)ЮЪЬтНтОі
ЕБ![]() а§зЊжС
а§зЊжС![]() Ш§ЕудкЭЌвЛжБЯпЪБ,жБНгаДГіЯпЖЮ
Ш§ЕудкЭЌвЛжБЯпЪБ,жБНгаДГіЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=Љx+4гызјБъжсНЛгкAЃЌBСНЕуЃЌOCЁЭABгкЕуCЃЌPЪЧЯпЖЮOCЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЃЌНЋЯпЖЮAPШЦЕуAФцЪБеыа§зЊ45ЁуЃЌЕУЕНЯпЖЮAP'ЃЌСЌНгCP'ЃЌдђЯпЖЮCP'ЕФзюаЁжЕЮЊ(ЁЁЁЁ)
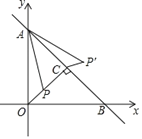
A.![]() B.1C.
B.1C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
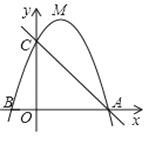
ЁОЬтФПЁПШчЭМЃЌЖЅЕуЮЊMЕФХзЮяЯпy=ax2+bx+3гыxжсНЛгкA(3ЃЌ0)ЃЌB(Љ1ЃЌ0)СНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкжБЯпACЕФЩЯЗНЕФХзЮяЯпЩЯЃЌгавЛЕуP(ВЛгыЕуMжиКЯ)ЃЌЪЙЁїACPЕФУцЛ§ЕШгкЁїACMЕФУцЛ§ЃЌЧыЧѓГіЕуPЕФзјБъЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
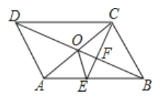
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЕФжаЕуЃЌНЋ
БпЕФжаЕуЃЌНЋ![]() ШЦ
ШЦ![]() Еуа§зЊ
Еуа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЯТСаНсТлЃКЂй
ЃЎЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЎЦфжае§ШЗЕФНсТлга______ЃЈжЛЬюаДађКХЃЉЃЎ
ЃЎЦфжае§ШЗЕФНсТлга______ЃЈжЛЬюаДађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтГѕжабЇЩњУПЬьдкаЃЬхг§ЛюЖЏЕФЪБМфЃЈЕЅЮЛЃКhЃЉЃЌЫцЛњЕїЫСЫИУаЃЕФВПЗжГѕжабЇЩњЃЎИљОнЕїВщНсЙћЃЌЛцжЦГіШчЯТЕФЭГМЦЭМ1КЭЭМ2ЃЎЧыИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
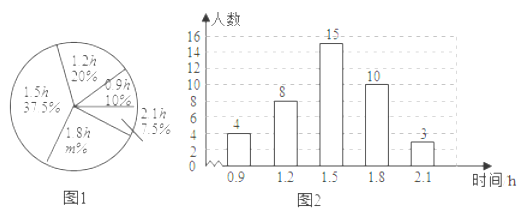
ЃЈЂёЃЉБОДЮНгЪмЕїВщЕФГѕжабЇЩњШЫЪ§ЮЊЁЁ ЁЁЃЌЭМ1жаmЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈЂђЃЉЧѓЭГМЦЕФетзщУПЬьдкаЃЬхг§ЛюЖЏЪБМфЪ§ОнЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂѓЃЉИљОнЭГМЦЕФетзщУПЬьдкаЃЬхг§ЛюЖЏЪБМфЕФбљБОЪ§ОнЃЌШєИУаЃЙВга1200УћГѕжабЇЩњЃЌЙРМЦИУаЃУПЬьдкаЃЬхг§ЛюЖЏЪБМфДѓгк1hЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com