
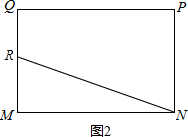
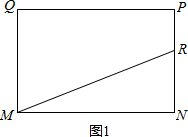
 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,| 1 |
| 2 |
| 1 |
| 2 |
 解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,
解:(1)如图1,∵点R运动的路程为x,△MNR的面积为y,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖北咸宁卷)数学(带解析) 题型:解答题
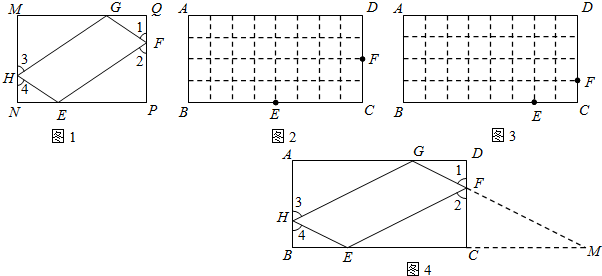
如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若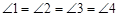 ,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且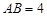 ,
, .
.
理解与作图:
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
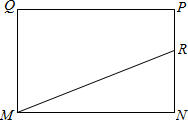 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com