
【题目】定义:对于已知的两个函数,任取自变量![]() 的一个值,当
的一个值,当![]() 时,它们对应的函数值相等;当
时,它们对应的函数值相等;当![]() 时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数
时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数![]() ,它的相关函数为
,它的相关函数为![]() .
.
(1)已知点![]() 在一次函数
在一次函数![]() 的相关函数的图像上,求
的相关函数的图像上,求![]() 的值;
的值;
(2)已知二次函数![]() .
.
①当点![]() 在这个函数的相关函数的图像上时,求
在这个函数的相关函数的图像上时,求![]() 的值;
的值;
②当![]() 时,求函数
时,求函数![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
(3)在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,连结
,连结![]() .直接写出线段
.直接写出线段![]() 与二次函数
与二次函数![]() 的相关函数的图像有两个公共点时
的相关函数的图像有两个公共点时![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)①![]() 、
、![]() ;②
;②![]() ,
,![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)先求出![]() 的相关函数,然后代入求解,即可得到答案;
的相关函数,然后代入求解,即可得到答案;
(2)先求出二次函数的相关函数,①分为m<0和m≥0两种情况将点B的坐标代入对应的关系式求解即可;
②当-3≤x<0时,y=x2-4x+![]() ,然后可 此时的最大值和最小值,当0≤x≤3时,函数y=-x2+4x-
,然后可 此时的最大值和最小值,当0≤x≤3时,函数y=-x2+4x-![]() ,求得此时的最大值和最小值,从而可得到当-3≤x≤3时的最大值和最小值;
,求得此时的最大值和最小值,从而可得到当-3≤x≤3时的最大值和最小值;
(3)首先确定出二次函数y=-x2+4x+n的相关函数与线段MN恰好有1个交点、2个交点、3个交点时n的值,然后结合函数图象可确定出n的取值范围.
解:(1)根据题意,
一次函数![]() 的相关函数为
的相关函数为![]() ,
,
∴把点![]() 代入
代入![]() ,则
,则
![]() ,
,
∴![]() ;
;
(2)根据题意,二次函数![]() 的相关函数为
的相关函数为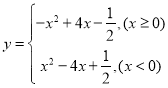 ,
,
①当m<0时,将B(m,![]() )代入y=x2-4x+
)代入y=x2-4x+![]() 得m2-4m+
得m2-4m+![]() ,
,
解得:m=2+![]() (舍去)或m=
(舍去)或m=![]() .
.
当m≥0时,将B(m,![]() )代入y=-x2+4x-
)代入y=-x2+4x-![]() 得:-m2+4m-
得:-m2+4m-![]() =
=![]() ,
,
解得:m=2+![]() 或m=2
或m=2![]() .
.
综上所述:m=![]() 或m=
或m=![]() 或m=
或m=![]() .
.
②当-3≤x<0时,y=x2-4x+![]() ,抛物线的对称轴为x=2,此时y随x的增大而减小,
,抛物线的对称轴为x=2,此时y随x的增大而减小,
∴当![]() 时,有最大值,即
时,有最大值,即![]() ,
,
∴此时y的最大值为![]() .
.
当0≤x≤3时,函数y=-x2+4x![]() ,抛物线的对称轴为x=2,
,抛物线的对称轴为x=2,
当x=0有最小值,最小值为![]() ,
,
当x=2时,有最大值,最大值y=![]() .
.
综上所述,当-3≤x≤3时,函数y=-x2+4x![]() 的相关函数的最大值为
的相关函数的最大值为![]() ,最小值为
,最小值为![]() ;
;
(3)如图1所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有1个公共点.
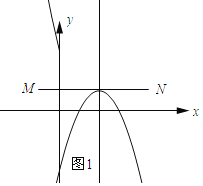
∴当x=2时,y=1,即-4+8+n=1,解得n=-3.
如图2所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点.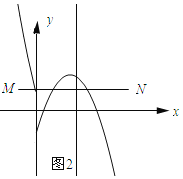
∵抛物线y=x2-4x-n与y轴交点纵坐标为1,
∴-n=1,解得:n=-1.
∴当-3<n≤-1时,线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点.
如图3所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点.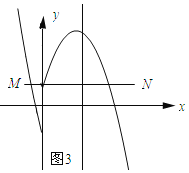
∵抛物线y=-x2+4x+n经过点(0,1),
∴n=1.
如图4所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点.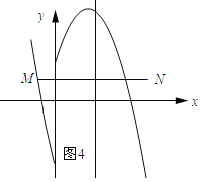
∵抛物线y=x2-4x-n经过点M(![]() ,1),
,1),
∴![]() +2-n=1,解得:n=
+2-n=1,解得:n=![]() .
.
∴1<n≤![]() 时,线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点.
时,线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点.
综上所述,n的取值范围是-3<n≤-1或1<n≤![]() .
.


科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
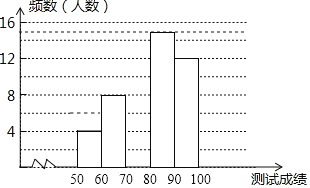
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
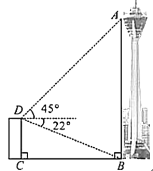
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张正面标有数字![]() ,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
(1)第一次抽到数字2的卡片的概率是 ;
(2)设第一次抽到的数字为![]() ,第二次抽到的数字为
,第二次抽到的数字为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请用树状图或列表法求点
,请用树状图或列表法求点![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平而直角坐标系中,已知点![]() ,直线
,直线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 恰好经过
恰好经过![]() 三点中的两点.
三点中的两点.
![]() 判断点
判断点![]() 是否在直线
是否在直线![]() 上.并说明理由;
上.并说明理由;
![]() 求
求![]() 的值;
的值;
![]() 平移抛物线
平移抛物线![]() ,使其顶点仍在直线
,使其顶点仍在直线![]() 上,求平移后所得抛物线与
上,求平移后所得抛物线与![]() 轴交点纵坐标的最大值.
轴交点纵坐标的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
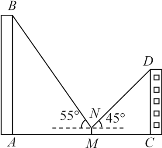
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油![]() 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
根据题中已有信息,解答下列问题:
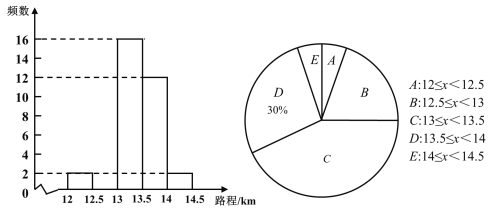
(1)求n的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车,试估计耗油![]() 所行使的路程低于
所行使的路程低于![]() 的该型号汽车的辆数;
的该型号汽车的辆数;
(3)从被抽取的耗油![]() 所行使路程在
所行使路程在![]() ,
,![]() 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的顶点A在反比例函数
的顶点A在反比例函数![]() 的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且
的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且![]() .
.

(1)若点E为线段OC的中点,求k的值;
(2)若![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,其面积小于3.
,其面积小于3.
①求证:![]() ;
;
②把![]() 称为
称为![]() ,
,![]() 两点间的“ZJ距离”,记为
两点间的“ZJ距离”,记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com