
��֪������![]() ��x���һ������ΪA(-1��0)����y�������ύ�ڵ�C��
��x���һ������ΪA(-1��0)����y�������ύ�ڵ�C��

1.ֱ��д�������ߵĶԳ��ᣬ����������![]() �����һ������B�����ꣻ
�����һ������B�����ꣻ
2.����ACB=90��ʱ���������ߵĽ���ʽ��
3.���������Ƿ���ڵ�M��ʹ�á�ABM�͡�ABC�������ȣ���ABM���ABC�غϳ��⣩�������ڣ���ֱ��д����M���ꣻ�������ڣ���˵�����ɣ�
4.�ڵ�һ�����ڣ����������Ƿ���ڵ�N��ʹ�á�BCN�������������ڣ����������ֵ�͵�N���ꣻ�������ڣ���˵�����ɣ�
1.�Գ����ǣ�ֱ��x=1����B��������(3��0)������������������ 2��
2.�ɡ�ACB=��AOC=��COB=90��á�AOC�ס�COB��
��![]() �� ��CO=
�� ��CO=![]() ����b��
����b��![]()
��![]() ʱ��
ʱ��![]() ��
��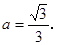 �� �������������� 4��
�� �������������� 4��
��![]()
3.��M�������ǣ���2��![]() ������1+
������1+![]() ��-
��-![]() ����1-
����1-![]() ��-
��-![]() ���������� 8��
���������� 8��
4.���N��������m��n������![]() ��
��
����N��ND��AB�ڵ�D�����У�
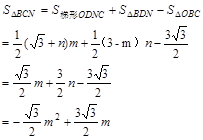
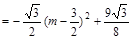 ������������������������ 10��
������������������������ 10��
��![]() ��0��
��0��
�൱![]() ʱ����BCN�����������ֵ��
ʱ����BCN�����������ֵ��![]() ��
��
��N������Ϊ![]() ������������������������ 12��
������������������������ 12��
����:��


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•���ޣ���ͼ����֪��������x���һ������A��1��0�����Գ�����x=-1�������������x�����һ���������ǣ�������
��2012•���ޣ���ͼ����֪��������x���һ������A��1��0�����Գ�����x=-1�������������x�����һ���������ǣ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009�����ʡʮ��������ʵ����ѧ���꼶���£�������ѧ�Ծ��������棩 ���ͣ������
 ��x���һ������ΪA��-1��0��
��x���һ������ΪA��-1��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012����б�ҵ��ѧ���ԣ�������������ѧ�������棩 ���ͣ�ѡ����
��ͼ����֪��������x���һ������A��1��0�����Գ�����x=��1�������������x�����һ���������ǡ� ��

����A������3��0������B������2��0������C��x=��3����D��x=��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�����ʡ�������п���ѧ�Ծ��������棩 ���ͣ�ѡ����
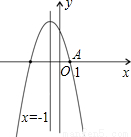
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
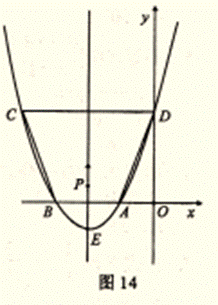
��ͼ14����֪������![]() ��x���һ������A������Ϊ��-1,0�����Գ���Ϊֱ�� x = 2.
��x���һ������A������Ϊ��-1,0�����Գ���Ϊֱ�� x = 2.
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㡣��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9.��������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�롣
�ٵ�tΪ ���ǣ���PAD���ܳ���С����tΪ ��ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
�ڵ�P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com