
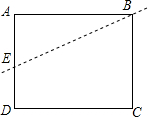
 如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$.
如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$. 分析 先根据题意画出图形,然后过A′作FG∥DC,交AD于F,交BC于点G.先由点A到DC的距离为1可求得BG、DF的长,依据勾股定理求得A′G的长,从而得到AF′的长,然后设AE=A′E=x,然后在△EFA′中,依据勾股定理可求得x的值.
解答 解;如图所示:过A′作FG∥DC,交AD于F,交BC于点G.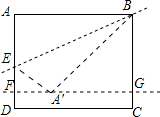
∵A′到DC的距离为1,FG∥DC,
∴FD=GC=1.
∴AF=BG=6.
由翻折的性质可知;AE=EA′,AB=A′B=10.
∵在Rt△A′BG中,A′G=$\sqrt{A{B}^{2}-B{G}^{2}}$=8,
∴AF′=2.
设AE=EA′=x,则EF=6-x.
∵在Rt△EFA′中,由勾股定理可知;EA′2=EF2+FA′2,即(6-x)2+22=x2,解得:x=$\frac{10}{3}$,
∴AE=$\frac{10}{3}$.
故答案为;$\frac{10}{3}$.
点评 本题主要考查的是勾股定理的应用、翻折的性质、点到直线的距离,依据勾股定理列出关于x的方程是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$)-1=3 | B. | (-2)3=8 | C. | (a-b)2=a2-b2 | D. | (a2)3÷a3=a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
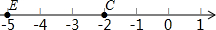 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )| A. | 26 | B. | 27 | C. | 28 | D. | 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
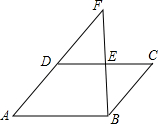 如图,E是?ABCD的边CD的中点,AD,BE的延长线交于点F,已知CE=2,?ABCD的周长等于14,则DF的长为( )
如图,E是?ABCD的边CD的中点,AD,BE的延长线交于点F,已知CE=2,?ABCD的周长等于14,则DF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com