
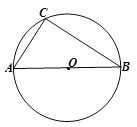
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
科目:初中数学 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.

例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2并研究该函数在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
(3)若函数y =![]() 与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式变形中,错误的是( )
A. 若a≥b,则a+c≥b+cB. 若a+c≥b+c,则a≥b
C. 若a≥b,则ac2≥bc2D. 若ac2≥bc2,则a≥b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.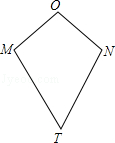
(1)探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=10,BC=CD,BC>AB,BD、AC为对角线,BD=16.
①若∠ABC=90°,求AC的长;
②过点B作BF⊥CD于F,BF交AC于点E,连接DE.当四边形ABED为菱形时,求点F到AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com