

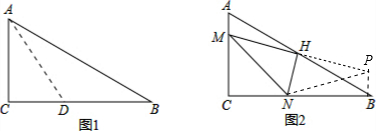
 解:(1)∵∠C=90°,AC=6,BC=8,
解:(1)∵∠C=90°,AC=6,BC=8,| PB |
| AM |
| PH |
| MH |
| BH |
| AH |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
| ||||
|
| 3 |
| 48 |
| 3 |
| (-4)2 |
| 75 |
5
|
| 108 |
|
| 2 |
| 3 | -64 |
| 1 |
| 4 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )
如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )| A、4cm | B、5cm |
| C、6cm | D、7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com