
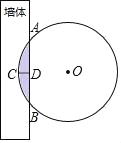
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在墙壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”问题题意为:如图,有一圆柱形木材埋在墙壁中,不知其直径大小.用锯去锯这木材,锯口深1寸(即CD=1寸),锯道长1尺(即AB=1尺),问这圆形木材直径是多少?(注:1尺=10寸)由此,可求出这圆形木材直径为______寸.
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
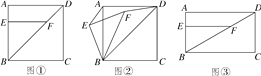
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
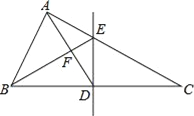
【题目】如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin (α-β)=sinαcosβ-cosαsinβ,
cos (α-β)=cosαcosβ+sinαsinβ
例:sin 15°=sin (45°-30°)=sin 45°cos 30°-cos 45°sin 30°=![]()
(1)试仿照例题,求出cos 15°的准确值;
(2)我们知道,tanα=![]() ,试求出tan 15°的准确值.
,试求出tan 15°的准确值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】转转盘和摸球是等可能概率下的经典模型.
(1)在一个不透明的口袋中,放入除颜色外其余都相同的4个小球,其中1个白球,3个黑球搅匀后,随机同时摸出2个球,求摸出两个都是黑球的概率(要求釆用树状图或列表法求解);
(2)如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
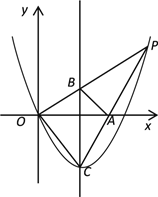
查看答案和解析>>
科目:初中数学 来源: 题型:
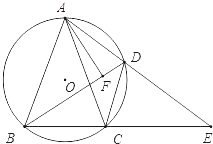
【题目】如图,△ABC内接于⊙O,且AB=AC,D是![]() 上一点,AD与BC交于E,AF⊥DB,垂足为F.
上一点,AD与BC交于E,AF⊥DB,垂足为F.
(1)求证:∠ADB=∠CDE;
(2)若AF=DC=6,AB=10,求△DBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
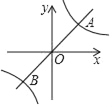
【题目】如图,一次函数y=x的图象与反比例函数y═![]() 的图象交于A,B两点,且点A坐标为(1,m).
的图象交于A,B两点,且点A坐标为(1,m).
(1)求此反比例函数的解析式;
(2)当x取何值时,一次函数大于反比例函数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com