练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列运算正确的是（　　）
    A．x2÷x3=x2B．（-2x）3=-6x3C．2x2-x=xD．（x3）3=x9

    分析 根据合并同类项法则、积的乘方、同底数幂的乘法和除法，对各项计算后即可判断．

    解答 解：A、x2÷x3=x-1，错误；
    B、（-2x）3=-8x3，错误；
    C、2x2与x不是同类项，不能合并，错误；
    D、（x3）3=x9，正确；
    故选D．

    点评 本题考查包括合并同类项、积的乘方、同底数幂的乘法和除法，需熟练掌握且区分清楚，才不容易出错．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．已知x、y、z均是非负实数，且满足x+3y+2z=3，3x+3y+z=4，则3x-2y+4z的最大值为7，最小值为-$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一个扇形的圆心角为144°，半径长为0.3m，小志好奇的思考着：这个扇形的周长是1.35cm （可以使用科学计算器，结果精确到0.01）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

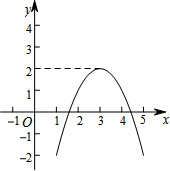    6．对某一个函数给出如下定义：如果存在实数M，对于任意的函数值y，都满足y≤M，那么称这个函数是有上界函数，在所有满足条件的M中，其最小值称为这个函数的上确界．例如，图中的函数是有上界函数，其上确界是2．
    （1）分别判断函数y=-$\frac{1}{x}$（x＜0）和y=2x-3（x＜2）是不是有上界函数？如果是有上界函数，求其上确界；
    （2）如果函数y=-x+2（a≤x≤b，b＞a）的上确界是b，且这个函数的最小值不超过2a+1，求a的取值范围；
    （3）如果函数y=x2-2ax+2（1≤x≤5）是以3为上确界的有上界函数，求实数a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

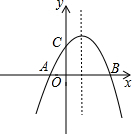    13．如图，已知二次函数y=-（x+1）（x-m）的图象与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，且图象经过点M（2，3）．
    （1）求二次函数的解析式；
    （2）求ABC的面积；
    （3）在抛物线的对称轴上找一点H，使AH+CH最小，并求出点H的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．小敏在“百度”搜索引擎中输入“水晶之都”，能搜索到与之相关的结果信息个数约为4460000，这个数用科学记数法表示为4.46×106．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2m，台阶AC的坡度为1：$\sqrt{3}$，且B、C、E三点在同一条直线上．请根据以上条件：
    （1）求出点A到点C的距离AC．
    （2）求出树DE的高度．（测量器的高度忽略不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

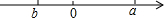    7．若实数a、b在数轴上的位置如图所示，则代数式|b-a|+$\sqrt{{a}^{2}}$化简为（　　）
    A．bB．b-2aC．2a-bD．b+2a

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图所示，四边形OABC是矩形，点A、C的坐标分别为（6，0），（0，2），点D是线段BC上的动点（与端点B、C不重合），过点D作直线y=-$\frac{1}{2}$x+m交折线OAB于点E．
    （1）若直线y=-$\frac{1}{2}$x+m经过点A，请直接写出m的值；
    （2）记△ODE的面积为S，求S与m的函数关系式；
    （3）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否分随着E点位置的变化而变化？若不变，求出重叠部分的面积；若改变，请说明理由．

    查看答案和解析>>

    同步练习册答案