
【题目】如图,已知∠AOB=90![]() ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4![]() 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1![]() 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180![]() 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.
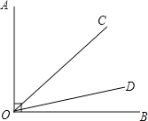
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30![]() 时,求旋转的时间.
时,求旋转的时间.
(3)当OB平分∠COD时,求旋转的时间.
【答案】(1)40°;(2)12秒或24秒;(3)30秒.
【解析】
(1)根据时间和速度分别得∠BOD和∠AOC的度数,由角的和与差可得结论;
(2)设转动t秒,OC与OD的夹角是30度,①如图1,列方程即可得到结论;②如图2,列方程即可得到结论;
(3)如图3,设转动m秒时,根据角平分线的定义列方程即可得到结论.
解:(1)当OC旋转10秒时,
∵射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转,
∴∠AOC=4×10=40°,
∵射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转,
∴∠BOD=1×10=10°,
∴∠COD=90°40°10°=40°.
故答案为:40°;
(2)设转动t秒,OC与OD的夹角是30度,
①如图1,4t+t=9030,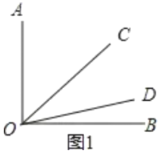
t=12,
②如图2,4t+t=90+30,
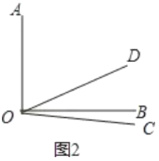
t=24,
∴旋转的时间是12秒或24秒;
(3)如图3,设转动m秒时,OB平分∠COD,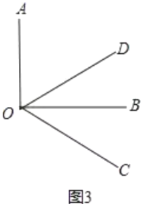
则4m90=m,
解得,m=30,
∴旋转的时间是30秒.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1),B(﹣1,1),C(0,﹣2).
(1)写出点B关于坐标原点O对称的点B1的坐标;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代数式表示:
(1)a,b两数的平方和减去它们乘积的2倍;
(2)a,b两数的和的平方减去它们的差的平方;
(3)一个两位数,个位上的数字为a,十位上的数字为b,请表示这个两位数;
(4)若a表示三位数,现把2放在它的右边,得到一个四位数,请表示这个四位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() .说明
.说明![]() 的理由.
的理由.
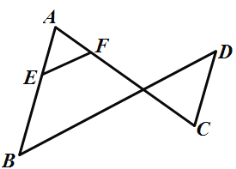
解:∵![]() (已知),
(已知),
∴________//________(_______________)
∴![]() (_______________)
(_______________)
∵![]() (________),
(________),
∴![]() (_______________)
(_______________)
∵![]() (己证),
(己证),
∴![]() (_______________).
(_______________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到![]() .请解答下列问题:
.请解答下列问题:
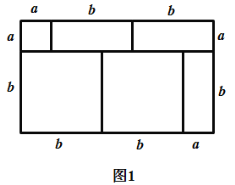
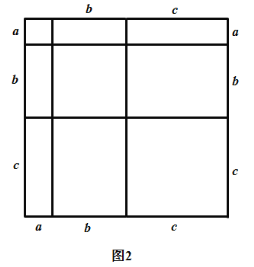
(1)仿照图1,构造适当的图形得到![]() 的值;
的值;
(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com