
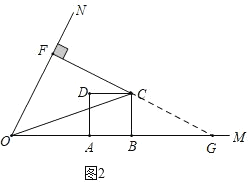
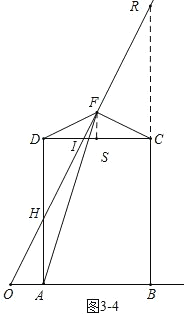
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
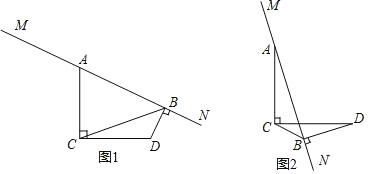
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
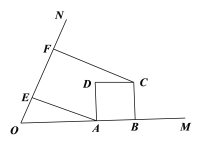
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
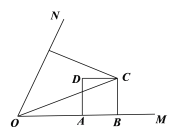
图(2)
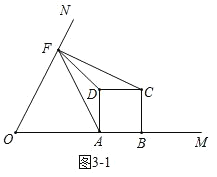
(3)如图(3),当△AFD与△CDF相似时,求m的值.
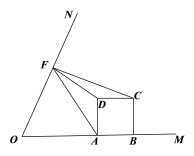
图(3)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)1或2或
;(3)1或2或![]() .
.
【解析】
(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则![]() ;
;
(2)如图2,延长FC交OM于点G,由(1)得![]() ,推出
,推出![]() ,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.
解:解:(1)如图1,
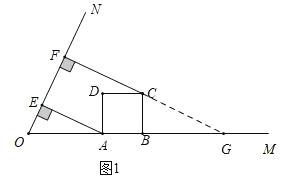
延长![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,
设![]() ,由
,由![]() ,
,
可得![]() ,则
,则![]() ,
,![]() ,
,
![]() ;
;
(2)如图2,
延长![]() 交
交![]() 于点
于点![]() ,由(1)得
,由(1)得![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由
中,由![]() ,
,
得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)当![]() 在
在![]() 内部时,
内部时,
①如图![]() ,
,
![]() 时,此时
时,此时![]() ,
,
![]() ;
;
②当![]() 时,
时,
如图![]() ,
,
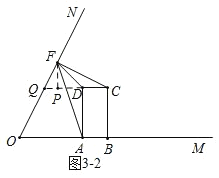
延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ;
;
当![]() 在
在![]() 外部时,
外部时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
如图![]() ,
,
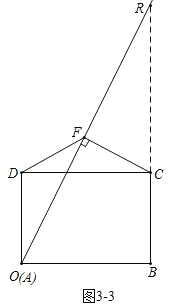
![]() 时,此时
时,此时![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() 重合,
重合,
延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
如图![]() ,
,
![]() 时,设
时,设![]() ,
,
延长![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得,![]() ,
,![]() (舍去),
(舍去),
![]() ,矛盾,
,矛盾,
综上所述:![]() 或
或![]() ,或
,或![]() .
.


科目:初中数学 来源: 题型:
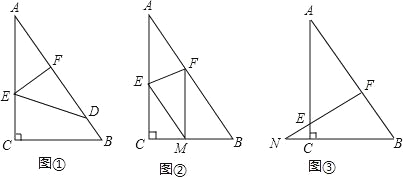
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是⊙O的内接三角形,AB为直径,AC=BC,D、E是⊙O上两点,连接AD、DE、AE.

(1)如图1,求证:∠AED﹣∠CAD=45°;
(2)如图2,若DE⊥AB于点H,过点D作DG⊥AC于点G,过点E作EK⊥AD于点K,交AC于点F,求证:AF=2DG;
(3)如图3,在(2)的条件下,连接DF、CD,若∠CDF=∠GAD,DK=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
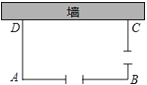
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
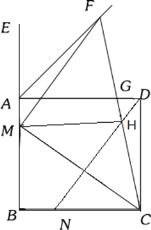
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC=DC,AC⊥DC,直线MN经过点A,作DB⊥MN,垂足为B,连接CB.
(1)直接写出∠D与∠MAC之间的数量关系;
(2)①如图1,猜想AB,BD与BC之间的数量关系,并说明理由;
②如图2,直接写出AB,BD与BC之间的数量关系;
(3)在MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,直接写出BC的值.
时,直接写出BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com