
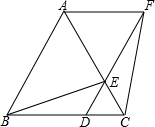
 如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,AB=6,BD=2DC,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.
如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,AB=6,BD=2DC,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.分析 (1)首先利用等边三角形的性质易得AB=BC=CA=6,∠ACB=60°,△EDC为等边三角形,过E作EG⊥DC于点G,易得∠GEC=30°,得GC=$\frac{1}{2}EC$=1,利用勾股定理可得EG,利用三角形的面积公式得结果;
(2)由∠AEF=∠CED=60°,EF=EA,易得△AEF为等边三角形,利用内错角相等,两直线平行易得AF∥BD,由AF=AE=AC-CE=BC-CD=BD,利用平行四边形的判定定理得出结论;
(3)过点A作AH⊥BC于H,易得∠BAH=30°,利用含30°直角三角形的性质,易得BH=$\frac{1}{2}AB=3$,利用勾股定理可得AH,代入S四边形ABEF=S四边形ABDF-S△BDE
=BD•AH-$\frac{1}{2}•BD•EG$,得出结论.
解答 解:(1)在等边△ABC中,
AB=BC=CA=6,∠ACB=60°,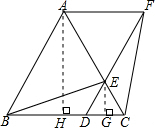
∵BD=2DC,CD=CE,
∴BD=4,CD=CE=2,
∴EDC为等边三角形,
过E作EG⊥DC于点G,
在Rt△EGC中,
∠ECG=60°,
∴∠GEC=30°,
∴$GC=\frac{1}{2}EC=1$,
∴$EG=\sqrt{E{C}^{2}-G{C}^{2}}$=$\sqrt{3}$
∴S△EDC=$\frac{1}{2}•DC•EG$=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$;
(2)四边形ABDF是平行四边形.
理由如下:
∵∠AEF=∠CED=60°,EF=EA,
∴△AEF为等边三角形,
∴∠AFE=∠FDC=60°,
∴AF∥BD,
∵AF=AE=AC-CE=BC-CD=BD,
∴AF∥BD且AF=BD,
∴四边形ABDF为平行四边形;
(3)过点A作AH⊥BC于H,
在Rt△ABH中,
∠BAH=90°-∠ABH=30°,
∴BH=$\frac{1}{2}$AB=3,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴S四边形ABEF=S四边形ABDF-S△BDE
=BD•AH-$\frac{1}{2}•BD•EG$
=$4×3\sqrt{3}-\frac{1}{2}×4×\sqrt{3}$,
=10$\sqrt{3}$.
点评 本题主要考查了等边三角形的性质及判定,平行四边形的判定,含30°直角三角形的性质,综合运用各种判定定理,作出适当的辅助线是解答此题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4-2$\sqrt{3}$ | B. | 2$\sqrt{3}$-4 | C. | -$\frac{2}{3}\sqrt{3}$ | D. | $\frac{2}{3}\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图
如图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com