
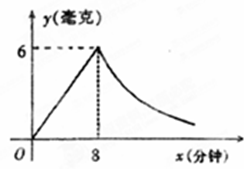
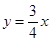 ,0≤x≤8,
,0≤x≤8,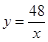 ;
;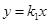 (k1≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧时y与x的函数解析式;由于在药物燃烧阶段后,y与x成反比例,因此设函数解析式为
(k1≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧时y与x的函数解析式;由于在药物燃烧阶段后,y与x成反比例,因此设函数解析式为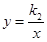 (k2≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;
(k2≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;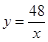 ,即可求得y的值,则可求得答案;
,即可求得y的值,则可求得答案;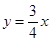 中得x="4," 把y=3代入
中得x="4," 把y=3代入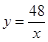 中得x=16,(8-4)+(16-8)=12>10得知此次消毒是无效的.
中得x=16,(8-4)+(16-8)=12>10得知此次消毒是无效的.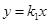 (k1≠0),函数的图象经过点P(8,6)
(k1≠0),函数的图象经过点P(8,6)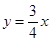 .自变量x的取值范围是0≤x≤8;
.自变量x的取值范围是0≤x≤8;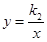 (k2≠0),函数的图象经过点P(8,6),
(k2≠0),函数的图象经过点P(8,6),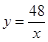 . 自变量x的取值范围是x≥4;
. 自变量x的取值范围是x≥4; 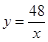 中得x="30,"
中得x="30," 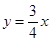 中得x=4,
中得x=4,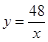 中得x=16,
中得x=16,

科目:初中数学 来源:不详 题型:填空题
 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 W.
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 W.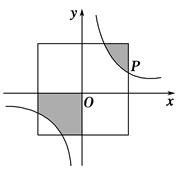
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
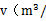 h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
h)与排完水池中的水所用的时间t(h)之间的函数关系图象. 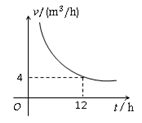
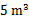 ,那么水池中的水要用多少小时排完?
,那么水池中的水要用多少小时排完?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若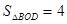 ,
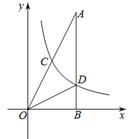
,
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
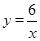 的图象上,则y1、y2、y3的大小关系是( )
的图象上,则y1、y2、y3的大小关系是( )| A.y3<y1<y2 | B.y1<y2<y3 | C.y2<y1<y3 | D.y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图像如图所示,点M是该函数图像上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( ).
的图像如图所示,点M是该函数图像上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( ).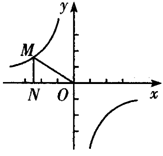
| A.-2 | B.4 | C.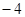 | D.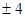 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com