
分析 分为两种情况,当∠AOB在∠AOC内部时,当∠AOB在∠AOC外部时,分别求出∠AOM和∠AOD度数,即可求出答案.
解答  解:分为两种情况:如图1,当∠AOB在∠AOC内部时,
解:分为两种情况:如图1,当∠AOB在∠AOC内部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°,
∵OD平分∠AOB,OM平分∠AOC,
∴∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°,∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°,
∴∠DOM=∠AOM-∠AOD=40°-10°=30°;
如图2,当∠AOB在∠AOC外部时,
∠DOM═∠AOM+∠AOD=40°+10°=50°;
故答案为:30°或50°.
点评 本题考查了角平分线定义的应用,用了分类讨论思想,解题的关键是掌握角平分线的意义.


科目:初中数学 来源: 题型:解答题
 已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.
已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | 5$\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
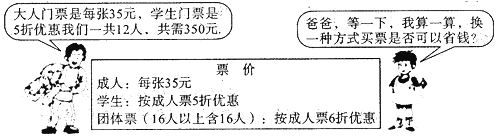
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com